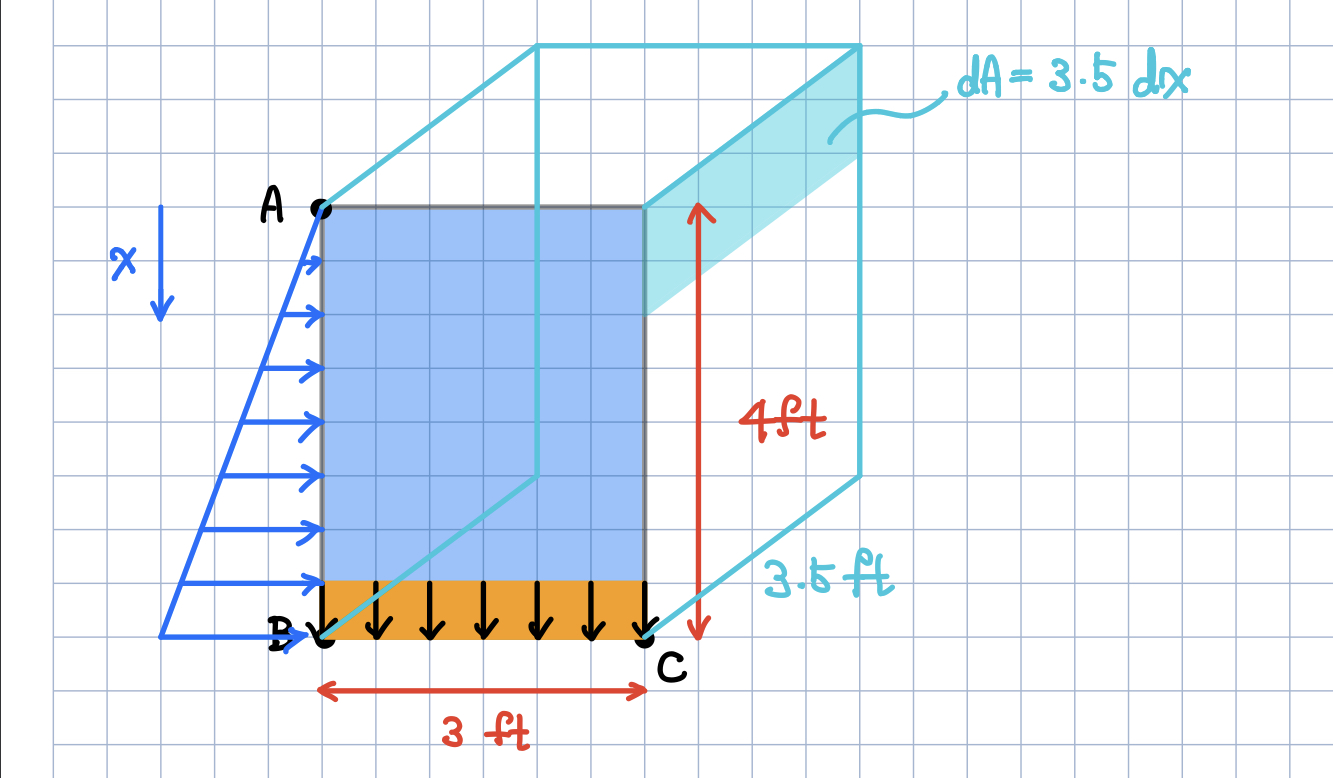
교수님 덕분에 재미있게 유체역학을 수강하고 있는 한 학생입니다 교수님. 다름이 아니라 가속도를 받는 유체에서는 힘을 구할때 전압력을 구할때처럼 비중량x높이 도심x면적으로 계산이 안되는 건가요?? 이 문제 같은 경우는 가속도를 받을때 압력을 구했는데 이 압력을 가지고 저 공식에 대입하고 싶은데 어떻게 적용을 해야할지 모르겠습니다
답변
질문의 요지는
정지 상태에서의 전압력이
가속도를 받는 유체에서의 힘을 구할 때 쓰이지 않는가 하는 점입니다.
일단,
전압력의 원리를 고민해보고,
가속도를 받는 유체에 작용하는 압력을 살펴보면
쉽게 질문에 대한 답을 얻을 수 있습니다.
유체역학 한방에 끝내기에서 강의했다시피
연직방향으로의 등가속도 운동을 받는 유체에는
아래와 같은 압력이 작용합니다.
\Delta{p} = \gamma h (1 + \frac{a_y}{g} )
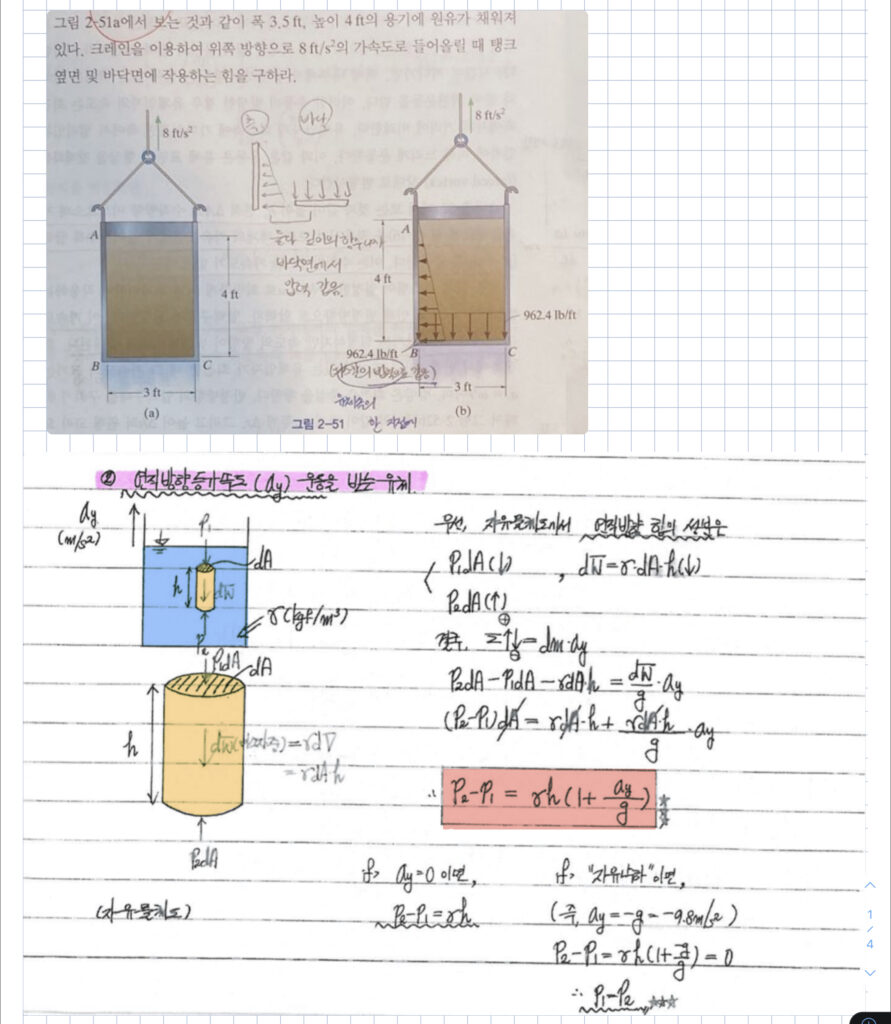
위의 내용을 이해해서 문제를 풀어봅시다.
아마 식에서 보실 때 느끼셨겠지만,
위의 압력은
- 전압력에 의한 압력
- 가속도에 의한 압력
두 압력의 합으로 이루어져 있습니다.
때문에 학생분의 질문에 자동적으로 답이 되는 것이죠.
가속도를 받는 유체에는
정지되어 있는 상태에서 받는 전압력도 받을 뿐 아니라
가속도에 의한 추가 압력을 받는 다는 것을 아셨을 겁니다.
압력은 하중을 넓이로 나눈 것이기 때문에
길이를 곱함으로써
분포하중을 계산할 수 있었고
삼각형 또는 사각형으로 작용하는 분포하중을
적분함으로써
면에 걸리는 전체 하중을 계산할 수 있는 겁니다.
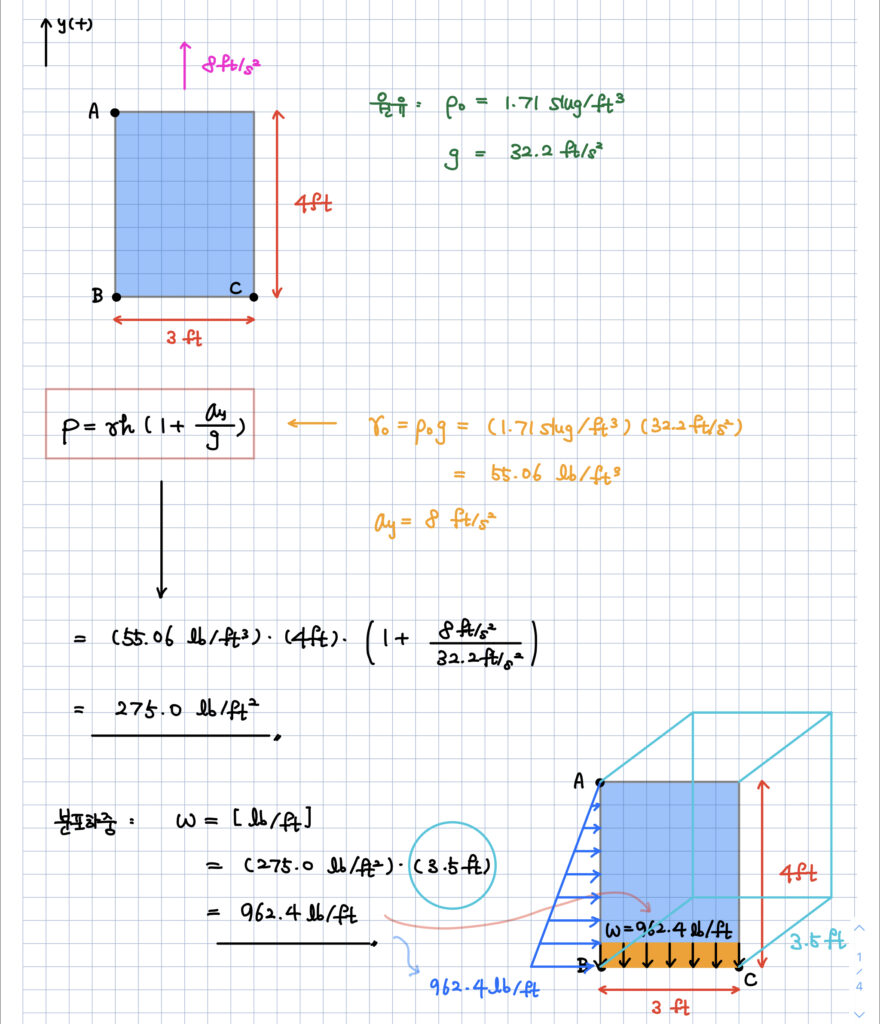
분포하중을 이용해서
각 면에 작용하는 하중을 계산하는 과정은 아래와 같습니다.

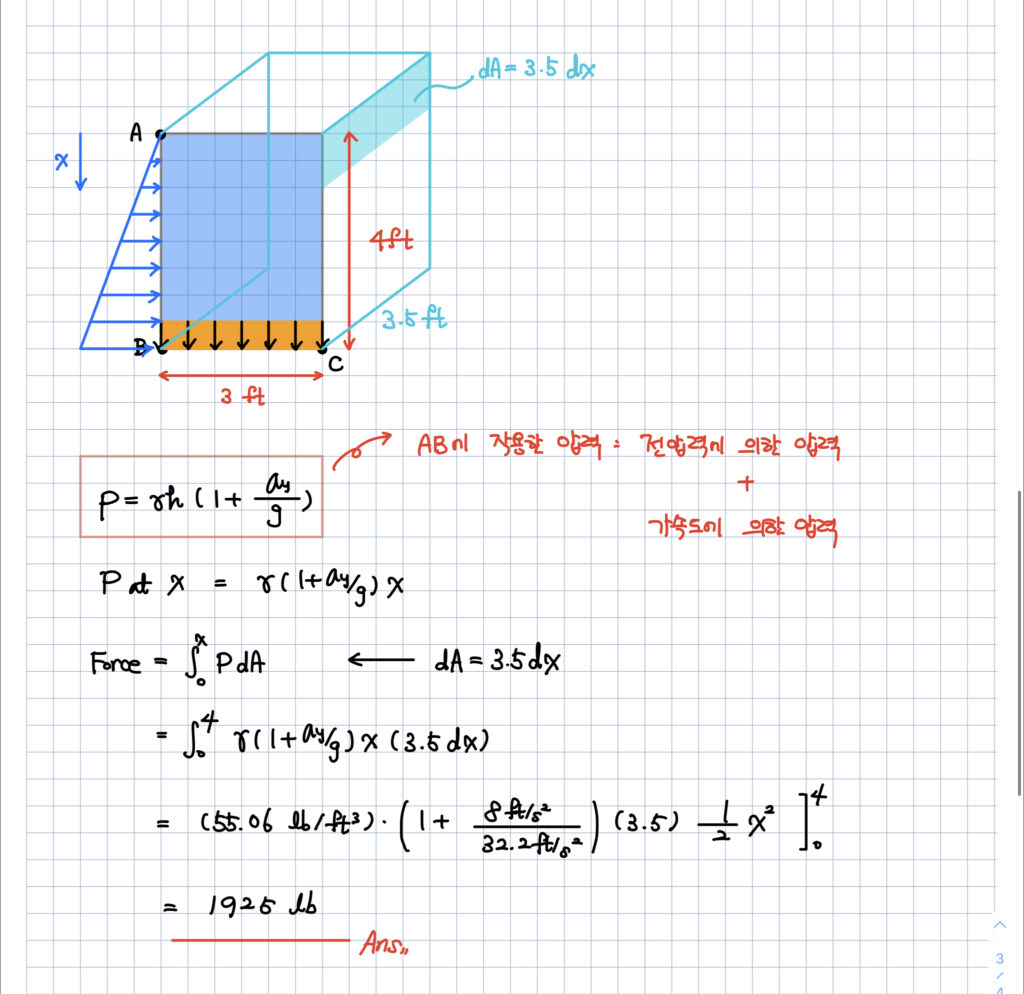
물론 아래와 같은 방법으로도 풀 수 있습니다.
임의의 x 지점에 따른 압력을 계산하고,
전체 하중은 임의의 지점 x 까지를 압력에 대해 적분하는 방법으로 말이죠.
물론 결과는 똑같이 나올 것입니다.
제가 아래에 빨간색으로 표시한 것처럼
수직방향으로 가속도를 받는
유체에 걸리는 압력은
정지상태에서의 전압력에 의한 압력과
가속도에 의한 압력의 합으로
계산된다는 것을 다시 한번 확인하시길 바랍니다.
질문에 대한 답이 됐기를 바랍니다.
물리적 현상에 대해
이런 케이스에 대한 식은 이것
저런 케이스에 대한 식은 저것
이런 식으로 암기하시기 보다는
제일 위해 제가 FBD 를 통해 유도했던 것과 같이
항상 백지 상태에서도
물리적인 현상을
kinetics 로 연결시킬 수 있도록 하시면 좋을 것 같습니다.
공부 열심히 하세요.
감사합니다.