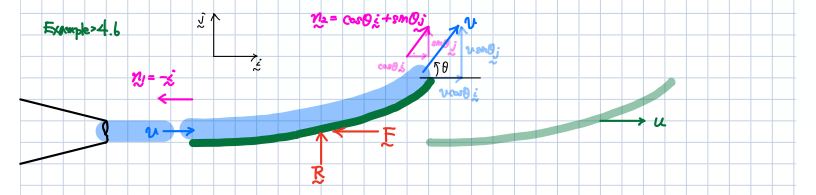
surface2를 푸실 때 ρA{(v-u)cosθi + (v-u)sinθj}{{(v-u)cosθi + (v-u)sinθj}●cosθi+sinθj}라고 하셨는데 저는 ρA{(vcosθ-u)i + vsinθj}{{(vcosθ-u)i + vsinθj}●cosθi+sinθj}가 들어가야 된다고 생각해서 그런지 잘 이해가 안가더라고요. 제가 어느부분에서 잘 이해를 못한건지 알려주실 수 있나요?
답변
상당히 좋은 질문입니다.
이렇게 생각해보는 것은 매우 중요하고, 충분히 있음직한 질문이라고 생각해요.
일단 상대속도가 없을 때 아래와 같이 유도되는 것은 강의를 통해 잘 배우셨을 거라고 생각합니다.
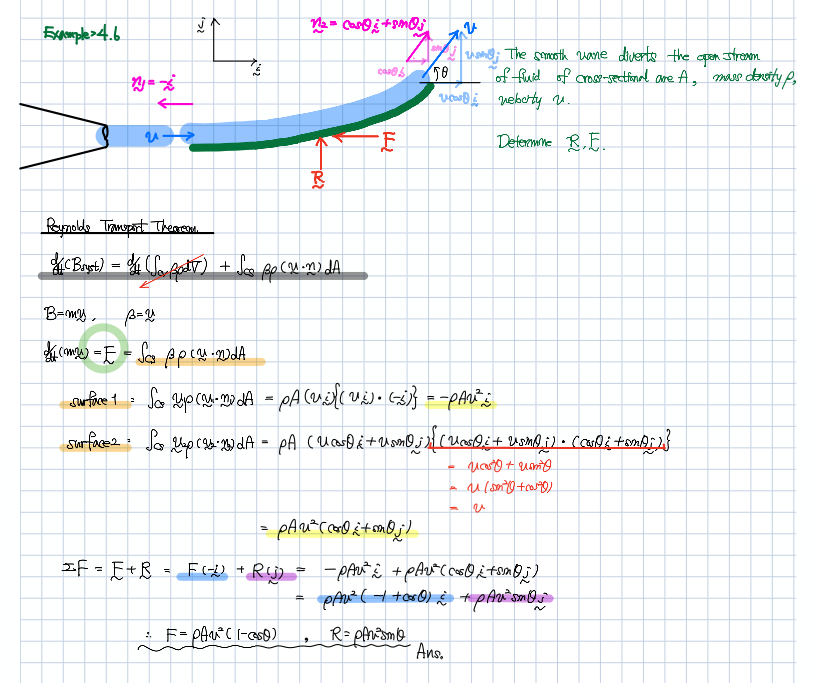
하지만 이와 같이 상대속도가 있을 때가 문제인데요.
상대속도인 u를 넣을 때
어차피 x방향 성분만 있으니까 cos\theta에 넣을 필요가 없이 밖으로 빼는 것이 맞지 않냐는 질문인데요.
만약에 일반적으로 외우는 공식을 이용해서
\Sigma \textbf{F} = m’ \Delta{\textbf{v}} : The relation between the resultant force on a steady-flow system and the corresponding mass flow rate and vector velocity increment
문제를 구할 경우
학생분께서 생각해주신대로 u 항을 아래와 같이 빼서 고민하는 것이 맞습니다.
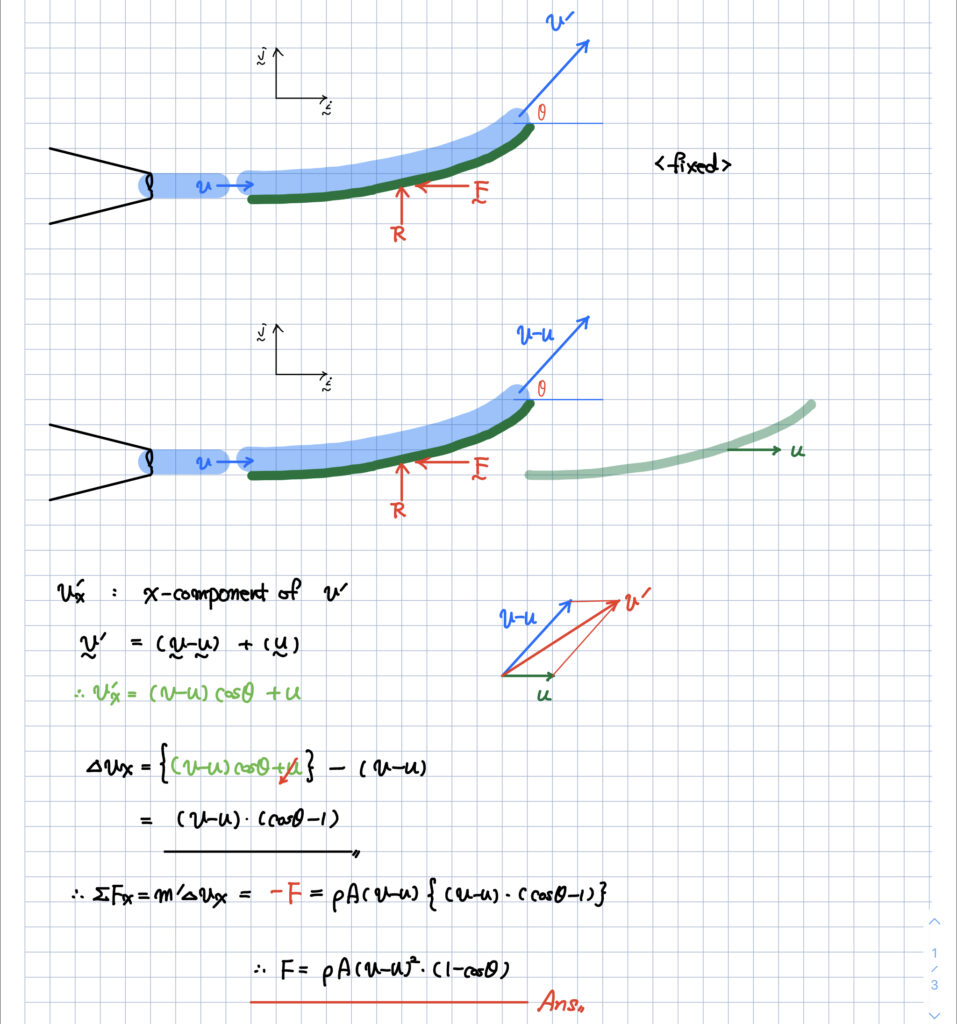
그런데 가급적 저는 공식 활용을 안하려고 하거든요.
공식을 외워봤자
조금만 문제가 응용되어도 못 푸는 경우가 많아서요.
때문에 아래와 같이 설명드렸습니다.
v-u를 이해하기 쉬운 가장 좋은 방법은
날개에 v 라는 속도로 유체가 들어간 상황에서
날개가 u 로 움직이고 있기 때문에
상대속도를 빼준 v-u라는 속도가 CV로 들어가고 나가는 속도라고 생각하시면 되겠습니다.
그렇다면 각각의 surface에서 아래와 같이 정리되어
일반적인 레이놀즈 수송정리를 이용하더라도
문제 없이 문제를 풀 수 있게 되죠.
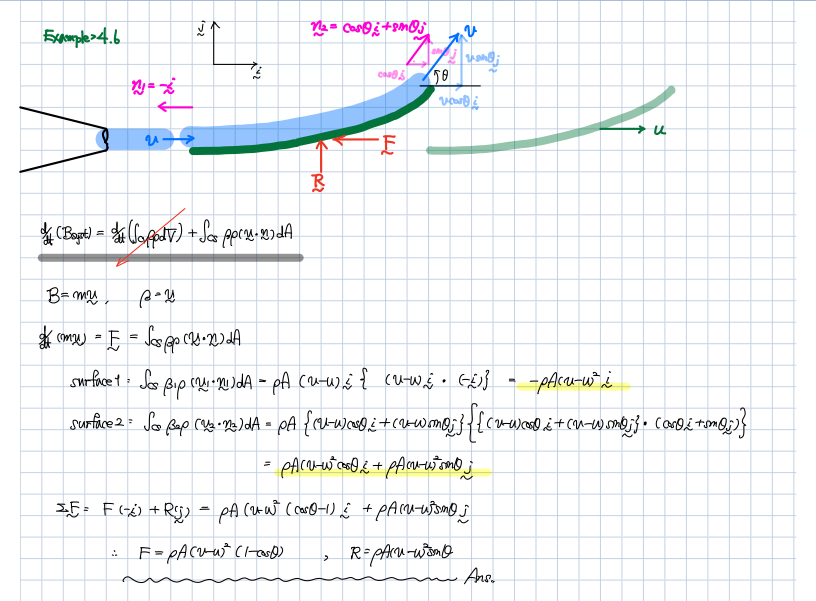
어떤 방법을 사용하든간에
잘 풀기만 하시면 되긴 하는데요.
제 경험 상 레이놀즈 수송정리에서 공식만 외워서 푸는 경우
시험 문제가 조금만 어렵게 나오면 풀지 못하는 경우가 왕왕 있더라구요.
둘다 잘 할 줄 알면 좋겠지만,
항상 레이놀즈 정리의 원리를 제대로 이해한 상태에서 문제를 푸실 수 있다면 좋겠습니다.