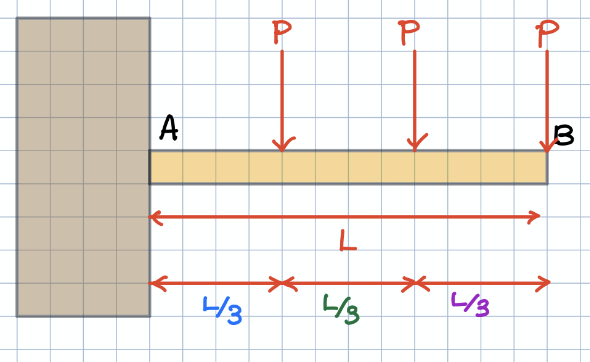
보의 SFD, BMD공부만 제대로 했다면 처짐각과 처짐량 구하는 것은 정말 쉬운데요. 생각보다 어려워하는 친구들이 많은 것 같습니다. 특히 하중이 하나가 아닌 다양한 하중이 같이 있을 때는 간단한 공식으로 해결이 쉽게 안되는 경우가 많다고 생각하는데요. 간단하게 몇 문제만 풀어보시면 금방 이해하실 수 있습니다!
하중이 하나인 외팔보
처짐과 처짐각은
모멘트를 구하는 것에서부터 시작합니다.
전단력과 모멘트의 부호규약에 대해서 헷갈리시는 분들이 많은데,
전단력의 경우 교재에 따라
오른쪽이 + 또는 – 인 경우가 있지만
처음 정한 부호규약대로만 잘 푸시면 전혀 문제가 없겠습니다.
저는 보통 크랜달 교재에 나와있는 방법을 이용해서
오른쪽 전단면의 전단력의 방향을 위로 +로 많이 하는데
이번에는 좀더 보편적인 방법인 아래를 +로 잡아보겠습니다.
(물론 처짐각과 처짐을 푸는 과정에서 전단력은 사용되지 않기 때문에 전혀 영향이 없습니다.)
가볍게 SFD, BMD를 그려주고
적분 몇번만 해주면,
처짐각과 처짐량을 계산할 수 있습니다.
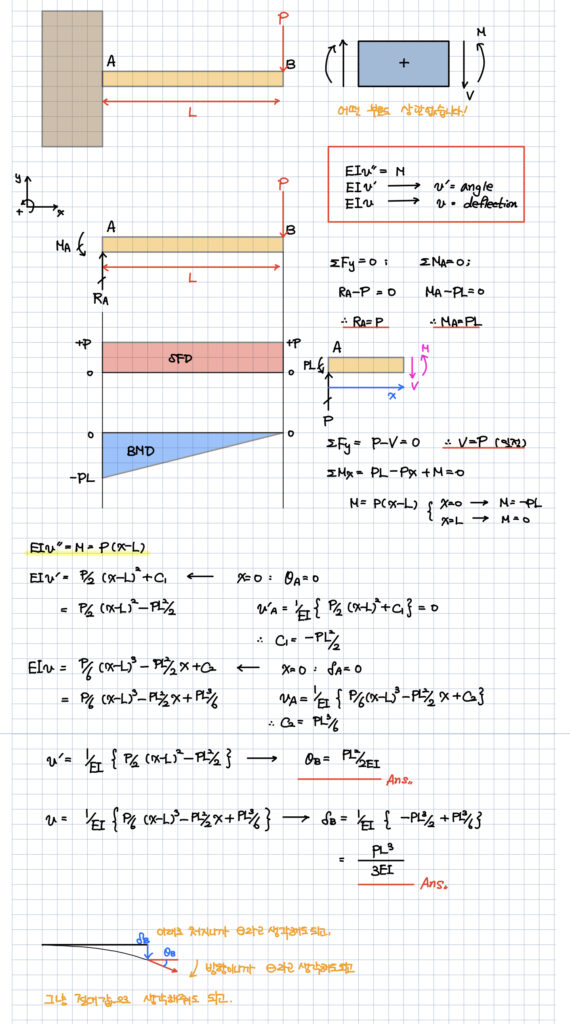
처짐각과 처짐량의 부호에 대해서 헷갈리시는 분들도 많은데,
학부과정에서는 그냥 편하게 절대값을 구해준다는 느낌으로 보면 편할 것 같습니다.
사실, coordinate의 +방향대로 나온 것이라…
시계반대방향이 +이기 때문에
아래의 해설과 같이 -의 처짐각이 나왔을 때
시계방향으로 처짐각이 발생한다고 볼 수 있고,
y방향이 위로 +이기 때문에
아래의 해설과 같이 -의 처짐이 발생했을 때
아래로 처짐량이 발생한다고 볼 수 있겠습니다.
이런 부분 때문에
저는 크랜달에서 설명하는 방법대로
모멘트와 전단력이 -관계,
모멘트와 처짐각이 -관계,
처짐각과 처짐이 -관계…
+/-/+/- 식으로 편하게 외워서 공부했는데,
학부 과정에서는 그냥 절대값을 취해주면 되기 때문에
편하게 적분하시는 게 가장 좋을 것 같습니다.
하중이 여러 개인 외팔보
위에서 공부한 것을 잘 응용하면,
아래와 같이 multiple load 상황의 문제도 쉽게 풀 수 있습니다.
중첩의 원리를 적용함과 동시에,
공식을 사용하기 보다는
처짐각과 길이와의 곱으로
추가 처짐량을 계산하여 더해주는 방식을 사용했습니다.
저는 공식을 외워서 푸는 것을 지양하기 때문에
아래와 같이 기억하는 것은
간단한 문제를 풀 때 매우 도움이 될 수 있겠습니다.

분포하중과 집중하중이 결합된 형태의 단순보
마지막 문제로
distributed load와
point load가 결합된
simple beam의 처짐량을 계산해보도록 하겠습니다.
모멘트 구하는 것은 너무 쉽죠?
아래와 같이 쉽게 계산해줍니다.
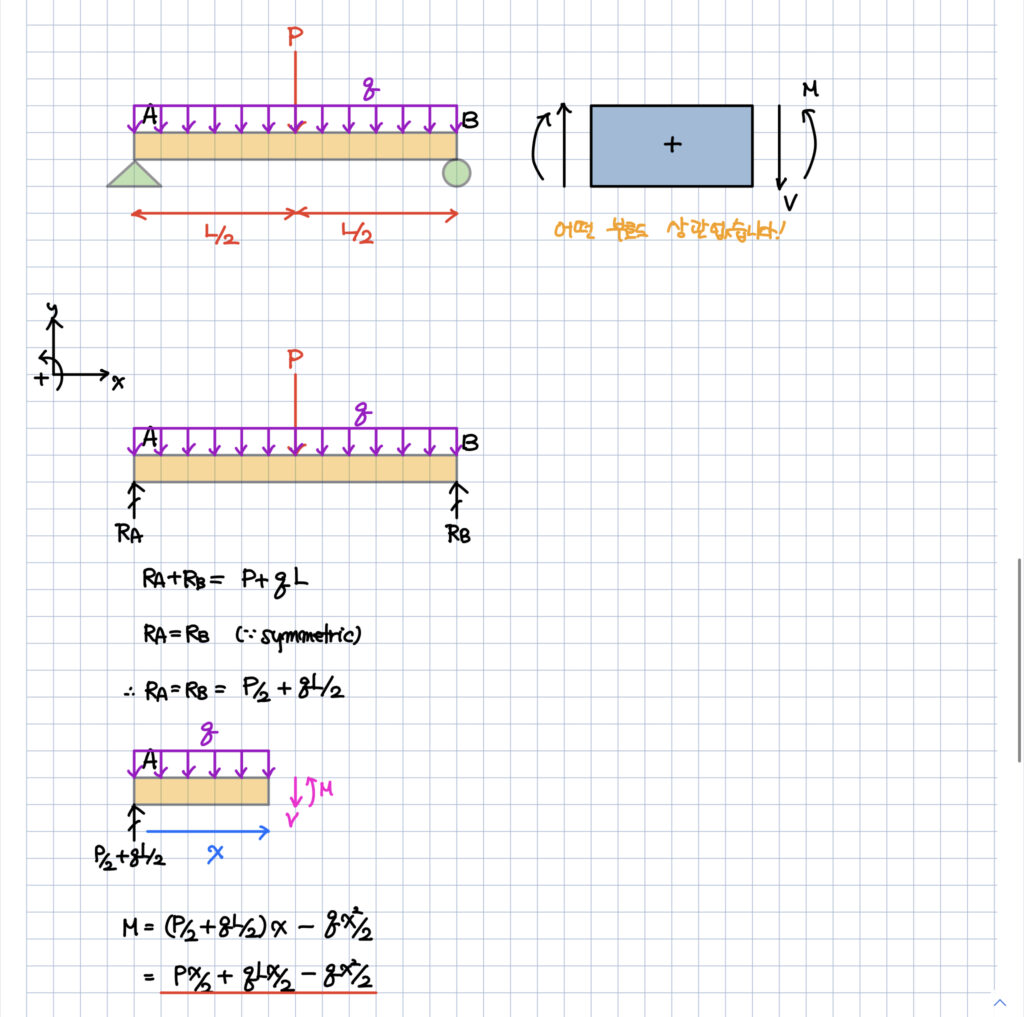
처짐량을 구하는 방법에는 여러 개가 있지만,
가장 적용이 편한 것은 아래의 2가지 방법입니다.
- 카스틸리아노 정리
- 중첩의 원리
고체역학 한방에 끝내기 또는 이전 포스팅에 설명한 바 있으니
링크를 통해 꼭 공부해보시길 바랍니다.

공식을 외워서 푸는 방법은
간단할 수는 있지만,
공식을 외워야 한다는 부담이 있기 때문에
시험대비용으로 공부하시면 좋을 것 같습니다.
보에 발생하는 처짐각 또는 처짐량에 대한 공식은
책 appendix 또는 인터넷에서 쉽게 찾으실 수 있으니 직접 필요한 공식을 찾아보시길 바랍니다.