질문
열전달량 구할때, q= u +pdv = h-vdp 에서, 밀폐계에서도 h-vdp 를 사용하실 수 있다고 하셨는데,
그러면 개방계에서는 q=u+pdv 를 못쓰는 거 맞나요? 왜냐하면 u+pdv 는 밀폐계에서의 에너지 평형으로부터 유도된 식이여서 안된다고 생각했는데 제말이 맞는지 확인해주시면 감사드리겠습니다.
답변
참 중요한 질문이고 많은 학생들이 질문했던 질문입니다. 열역학을 처음 공부하는 학생들에게 당연히 나올 수 있는 질문이고 개념을 정확하게 이해하는 데에 중요한 내용이라 생각합니다.
답변에 앞서 제가 이전에 했던 관련 답변을 아래에 첨부했으니 먼저 읽어주시면 감사하겠습니다.
https://godjunpyo.com/밀폐계에서도-엔탈피-사용이-가능한가-질문번호-0943/
보셨다시피 아래의 두 식 모두 열역학 1법칙에 근거하여 유도된 것임을 아실 수 있습니다.
\delta{q} = du + p dv = dh – v dp (열역학 1법칙 관련 식)
밀폐계를 예로 들어보겠습니다. 일단 두 식을 모두 사용하는 것은 열역학 1법칙에 위배되지 않으니까 괜찮다고 생각해보겠습니다.
밀폐계에서 정적과정 중 열전달이 있었다면 내부에너지의 변화로 아주 쉽게 열량을 계산할 수 있습니다.
\delta{q} = du = C_v dT (정적과정: dv=0)
이 물리적 의미를 잘 생각해보면, 시스템이 열(=에너지)을 받는다면 팽창하면서 일을 해야 하는데, 정적과정이라 기계적인 일을 하지 못하고 에너지를 그 한정된 공간에서 쌓아놓는 겁니다. (마치 배터리가 충전되는 것처럼요.) 물질의 에너지의 정도는 내부에너지로써 측정이 가능하기 때문에 정적과정에서의 열은 모두 내부에너지가 증가하는 데에 사용되는 것이죠.
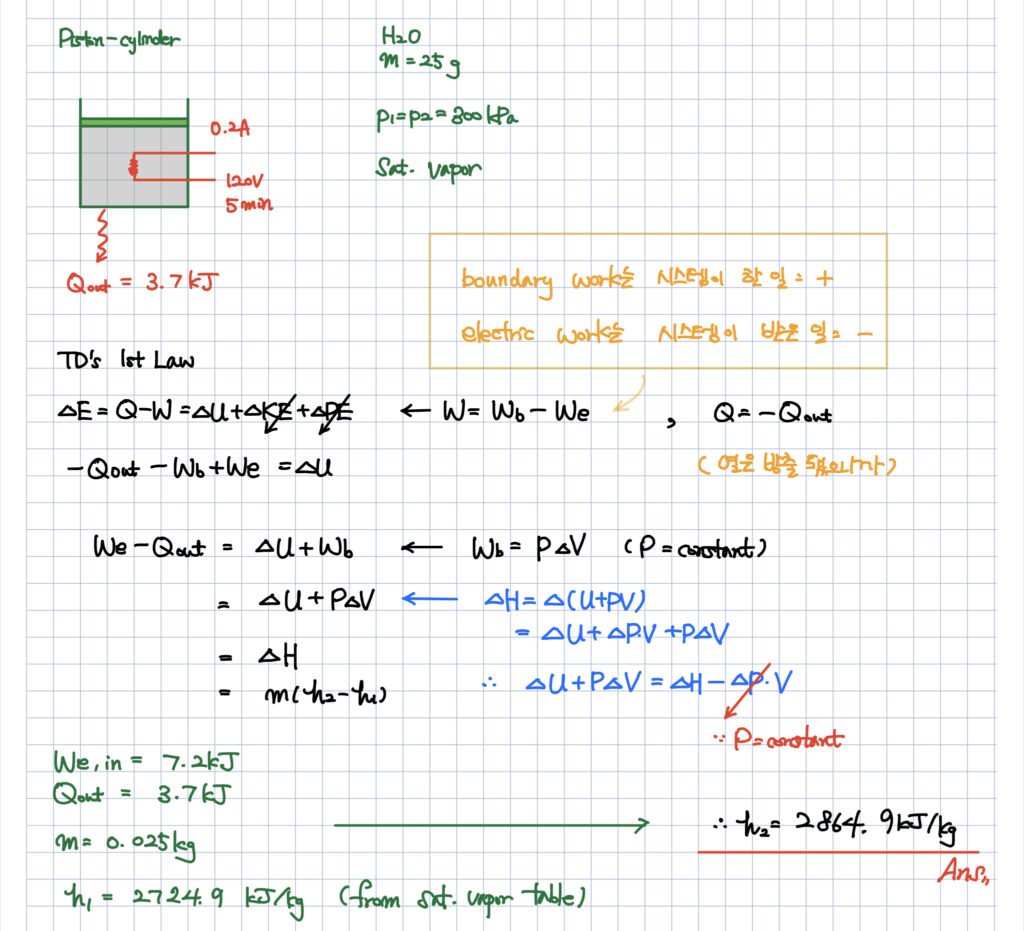
그러면 밀폐계에서는 무조건 내부에너지 관련 식만 이용해야할까요? 아닙니다. 상황에 따라 엔탈피 관련 식이 더 쉽다면 엔탈피 식을 이용할 수도 있죠. 예를 들어 등압과정으로 팽창하는 상황이라면 내부에너지보다는 엔탈피 관련 식을 이용하는 것이 훨씬 더 편할 겁니다. 간단한 예제를 아래에 참고로 보여드리겠습니다.
제가 이러한 질문에 대한 대답으로 드릴 수 있는 것은 열역학 1법칙에 근거하여 문제의 조건에 따라 가장 문제를 쉽게 풀 수 있는 방법으로 푸는 것이 중요하다는 겁니다. 절대적으로 이런 상황에서는 이런 식, 저런 상황에서는 저런 식이라는 규칙이라는 것은 없습니다.
다시 질문으로 돌아가서, 개방계에서 아래처럼 굳이 내부에너지 식을 써야하는 이유가 있으실까요?
\delta{q} = u+ pdv (내부에너지 관련 식)
일단 위의 내부에너지 식은 boundary work만 고려된 상황이기 때문에 유동에너지 항도 추가하고, 운동/위치에너지도 고려해주셔야만 사용하실 수 있습니다. 개방계에 대한 해석은 우리가 control volume을 이용해서 시스템의 부피가 일정하다고 생각하여 엔탈피 관련 식을 쓰고 개방계에서의 일량식을 쓰는 것이 일반적입니다. 물론 내부에너지로도 구할 수 있겠지만, 쉽게 갈 수 있는 방법을 굳이 돌아갈 필요는 없는 것이죠.
요약하자면, 열역학 1법칙에 근거해서 구하면 어떤 계이든지 전혀 문제 없이 구할 수 있을 겁니다. 중요한 것은 문제의 조건에 따라 가장 쉽게 계산할 수 있는 방법을 잘 선택하는 것이죠.
제가 올려드린 추가 예제 등과 위의 답변을 통해 궁금증이 조금은 해소되기를 바랍니다. 감사합니다.