비회전 좌표계와 회전 좌표게에서 속도, 가속도 질문

일단 수학적으로도 왜 비회전좌표계와 회전 좌표계에서 관측한 상대 속도가 다르고, 어떻게 그 공식이 나오는 지는 알겠고, 이것 때문에 겉보기 힘(원심력)을 회전하는 좌표계에서 추가적으로 고려해주어야한다는 것 까지는 순조로운데요,,

문제는 이 부분부터입니다.

첫 번째 질문:

단 저기서 P라는 점을 왜 고려해야 하는 지를 모르겠습니다. 그리고 그 P라는 점은 왜 하필 관찰하는 순간에 A와 같은 지점을 지나는 점이어야 하는 걸까요. A와 다른 점이 대체 뭐길래 저렇게 해석해야하는거죠?

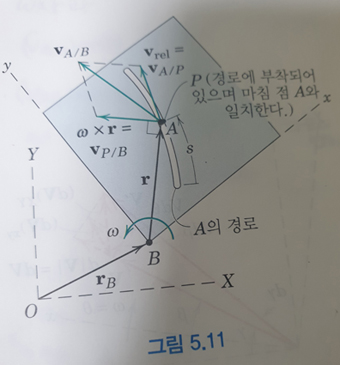
두 번째 질문:

(Vrel은 회전 좌표계에서 본 B에 대한 A의 상대 속도, Va는 비회전 좌표계에서 본 A의 속도, Vb는 B의 속도, ω는 회전 좌표계의 각속도, r은 기준점 B에서부터 A까지의 위치벡터)

라는 공식에서, 책에는 ω x r은 $v_{P/B}$ 이며 Vrel은 $v_{A/P}$ 라고 되어 있습니다. 이 부분도 왜 그런지 이해가 안되네요. 아마 1번부터 막혀서 그런 것 같긴 한데 이 부분도 설명해 주셨으면 좋겠습니다.

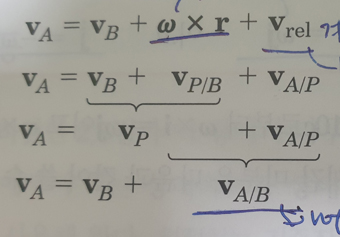
세 번째 질문:

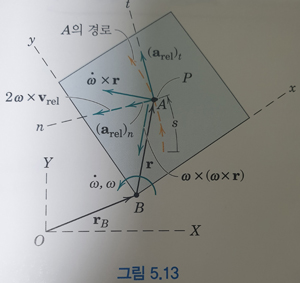
마찬가지로 같은 질문이지만 상대 가속도 부분입니다.

$a_{P/B}$ , $v_{A/P}$ 부분이 이해가 되지 않습니다.

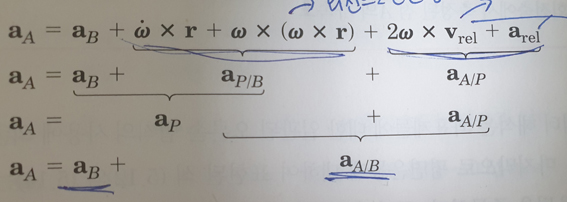
답변 (첫 번째 질문)

첫 번째 질문:

안녕하세요.

너무 아쉬운 내용의 질문입니다.

제가 30강에서 정말 자세하게 설명한 것인데,

혹시 강의를 들으셨는지 의심될 정도의 질문입니다.

많은 학생들이 위와 같은 그림과

복잡해 보이는 식들로 인해

동역학에서 어려움을 느끼고 있다는 것을 잘 알아서

책에 있는 공식 하나도 쓰지 않고 일일이 유도해드렸던 것 같은데

잘 와닿지 않은 것 같습니다.

아시겠지만, 이 내용의 핵심은 회전축 상에서의 물체의 운동을 해석하는 것입니다.

지구가 고정되어 있다고 가정하고,

꼬마 아이가 길을 걸어가고 있습니다.

이 내용은 만약 학생분이 회전목마를 타고 있을 때 그 꼬마 아이가 어떻게 보이는지를 알아내는 내용입니다.

때문에 이 강의 마지막에는

멈춰있는 것 같았던 우리 지구가

사실은 회전하고 있기 때문에

우리 입장에서 재밌게 보이는 현상인

“코리올리 효과” 등을 증명할 수 있었죠.

즉, 여기서 P 라는 점은 A 점과 같은 점이지만

절대계에서 보는 A와 다르게 두기 위해서

P라고 책에서는 다시 정의를 한 것입니다.

답변 (두 번째 질문)

두 번째 질문:

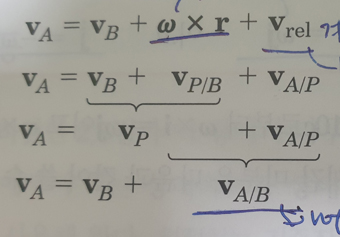
29강 상대속도를 강의했을 때도 설명드렸다시피,

$\omega \times r$ 이 $v_{P/B}$ 가 되는 이유는

P가 B를 중심으로 회전한다고 했을 때의 속도가 $\omega \times r$ 로 유도될 수 있기 때문입니다.

우리는 회전하는 축을 기준으로 움직이는 P를 관측하고 있기 때문에

상대속도 개념이 들어가야 올바르게 유도가 될 수 있겠습니다.

아래엔 우리가 29강에서 배웠던 내용입니다.

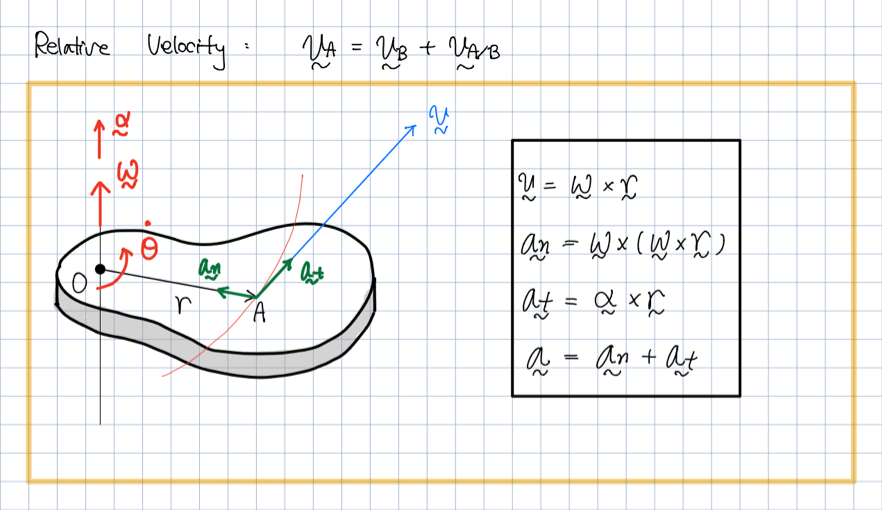
전반적으로 제가 이렇게 공부하면 너무 어렵고,

위의 식에 대해서 학생들이 이해도 안하고 외워버리거나 공부하지 않는 것이 너무 안타까워

아래와 같이 일일이 유도를 해드렸습니다.

제가 가르쳐드린대로

그냥 회전하는 축을 기준으로 어떤 물제를 본다는

상대속도와 상대가속도의 개념을 이해한다면

위에 질문하셨던 것처럼 복잡한 그림이나 식들이 하나도 필요없이도

쉽게 내용을 증명하실 수 있습니다.

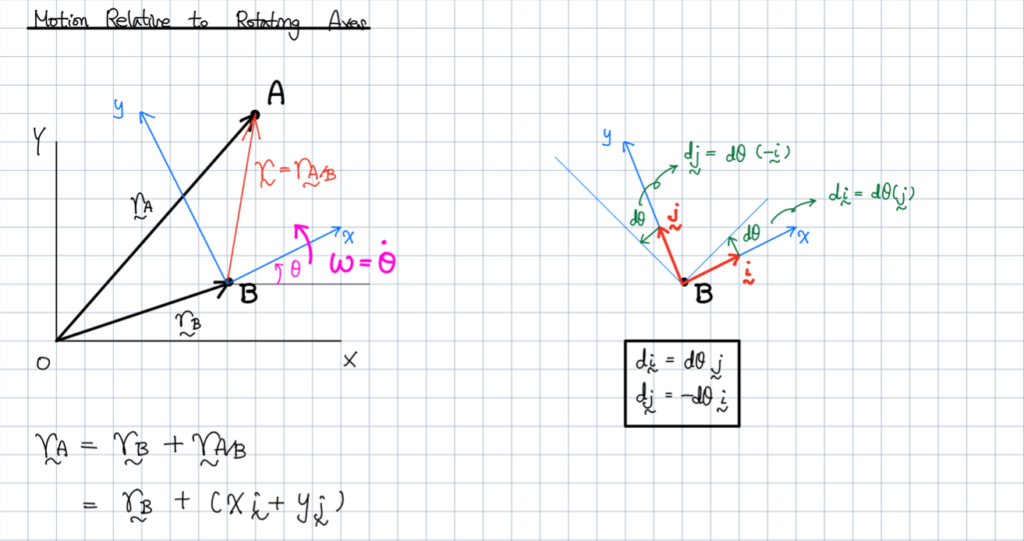
상대속도 개념을 적용하는 것과 동시에

우리는 회전하는 축의 단위벡터를 미분하는 과정을 통해

위의 그림을 해석한 바 있습니다.

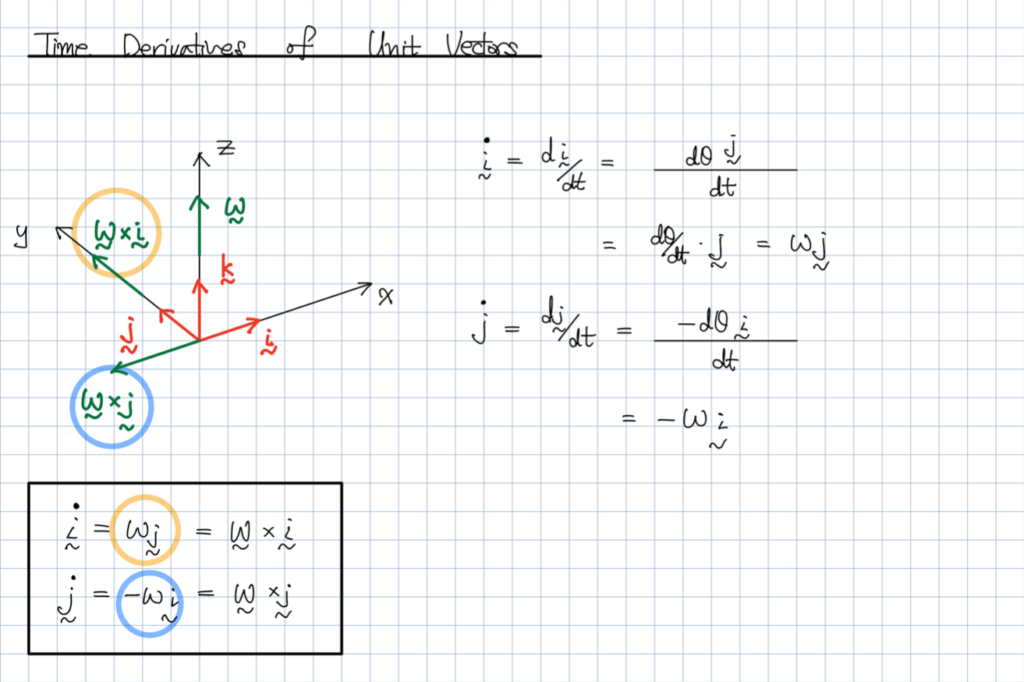
위와 같이 미분하는 과정만 이해할 수 있다면,

기존의 A와 B를 이용한 절대좌표계의 상대속도 개념만을 가지고도

회전하는 축에서의 A와 B를 이용한 (책에서는 P와 B) 상대속도 개념을 쉽게 유도할 수 있었습니다.

30강에서 다 설명했던 부분이기 때문에

만약 조금이라도 이해가 안되셨다면

몇번이고 반복해서 듣고

스스로 유도해보시면서

내 것으로 꼭 만들어내시길 바랍니다.

답변 (세 번째 질문)

세 번째 질문:

마찬가지로 같은 질문이지만 상대 가속도 부분입니다.

$a_{P/B}$ , $v_{A/P}$ 부분이 이해가 되지 않습니다.

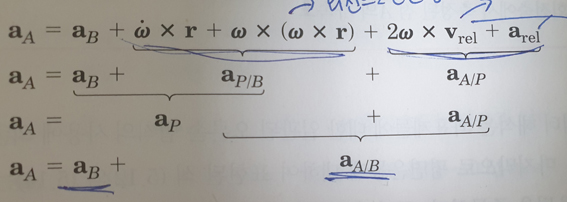
마지막 질문은 아마

위의 질문들과 내용을 이해하셨다면 충분히 이해하실 수 있을 것 같습니다.

가속도는 전혀 어려운 개념이 아닙니다.

변위를 시간에 대해서 한 번 미분한 것이 속도라면,

속도를 시간에 대해서 한 번 미분한 것이 가속도입니다.

회전축에 대한 상대속도를 우리가 유도할 줄 알았다면,

이 속도 벡터를 미분하여 상대 가속도 또한 쉽게 유도할 수 있습니다.

물론 여기서는 내가 활동하는 세계의 좌표계가 회전하고 있기 때문에

좌표계의 미분값이 0가 되지 않는다는 것을 주의해야 겠지만,

위의 질문에서 상대속도를 공부할 때도

잘 유도했기 때문에

상대 가속도도 같은 방법으로 하시면 유도하실 수 있으실 겁니다.

아래에 단위벡터의 미분뿐만 아니라

상대속도의 모든 항에 대한 미분식을 잘 정리해두었으니

아래의 강의 내용을 다시 보시면서 공부해보시길 바랍니다.

$a_{P/B}$ , $v_{A/P}$ 부분이 이해가 어렵다고 하셨는데,

이또한 상대속도개념을 바탕으로 생각하면 유도가 되는 부분입니다.

우리가 10강에서 배웠던

상대속도의 기본 중의 기본 개념을 절대 잊지 마시길 바랍니다.

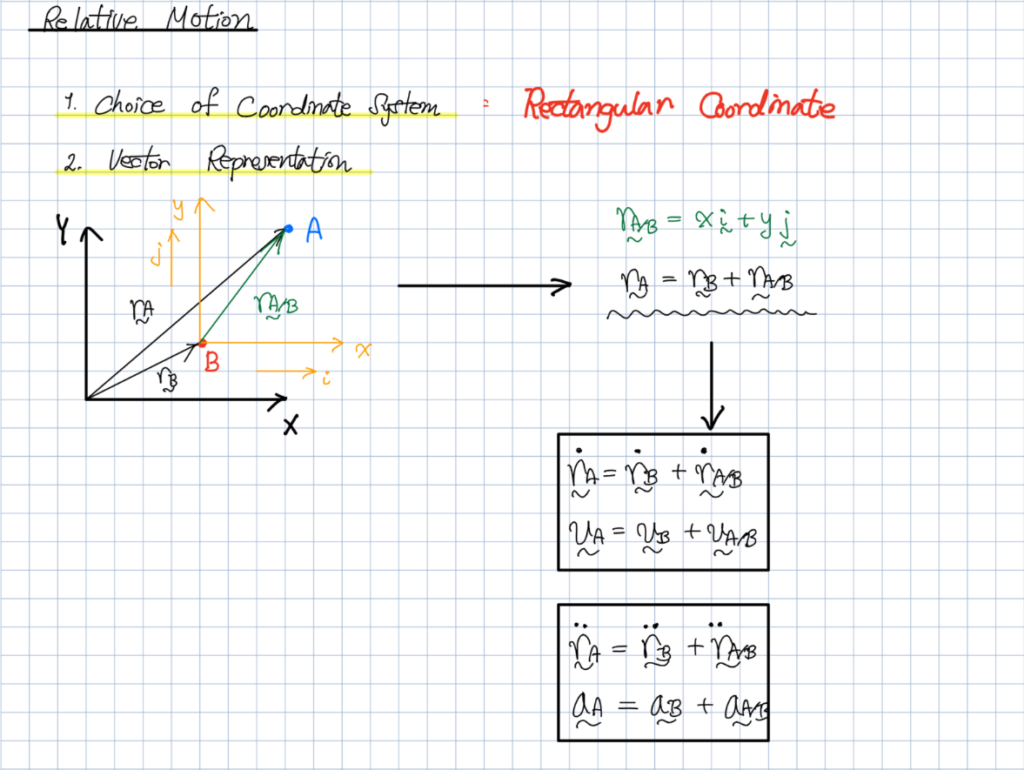
상대속도가 어려워 보이는 이유는

그냥 우리가 잘 안써와서 그렇습니다.

많이 사용해보지 않아서 그런 것이고

상대속도가 어려운 것이 아니라 우리 둘의 사이가 그냥 어색한 것일 뿐입니다.

하지만 제가 강의에서 얘기드린 것처럼,

A의 속도 = B의 속도 + B에서 본 A의 속도

라는 것만 잘 이해하셨다면,

뒤에 아무리 어려운 내용이 나와도 잘 이해하실 수 있으실 겁니다.

30강에서 다뤘던 내용을 모두 질문 주셔서 매우 안타깝습니다.

한 번 다시 들으시고,

빈 종이에 책을 보지 않고

다섯 번만이라도 유도해보세요.

저는 시험 공부할 때

책을 보지 않고 하나도 틀리지 않을 때까지 10번이고, 20번이고,

카페에서 지하철에서 버스에서

계속 머릿속으로 생각만 하면서 유도하면서 공부했습니다.

학생분께서도 그런 열정을 가지고 열심히 공부하실 수 있으셨으면 좋겠습니다.

만약 그렇게 연습했음에도 불구하고

이해가 되지 않는 부분이 생긴다면

언제든지 질문해주시길 바랍니다.

위의 답변들이 도움이 됐기를 바랍니다.

감사합니다.