고무줄을 잡아당기면 열이 방출됩니다. 고무줄이 열을 잃었다는 말이죠. 반대로 말하면 고무줄에 열을 공급하면 수축한다는 것을 알 수 있죠. 플라스틱이 불에 닿을 때 찌그러지는 것과 같죠. 근데 금속은 열이 올라가면 팽창하잖아요? 고무줄과 금속의 열에 대한 반응은 왜 다를까요?
답변
열역학에서 우리는 열역학 1법칙에 대해서 배웁니다.
간단히 말하면, 에너지의 변화는 계에 전달된 일과 열의 합이라는 것이죠.
이를 좀더 자세하게 풀어보면 아래와 같습니다.
dU = \delta{Q} – \delta {W} (열역학 1법칙)
\delta{W} = -f dl (Mechanical Work)
\delta{Q} = TdS (Entropy, assuming reversible)
dU = T dS + f dl (열역학 1법칙에 대입하면)
dl = \frac{1}{f} (dU – TdS) (dl 에 대해서 정리)
(\frac{\partial{l}}{\partial{T}})_{f,V} = \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} – \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} (최종식)
조금 복잡했죠?
마지막 식에 주목할 필요가 있는데요.
(\frac{\partial{l}}{\partial{T}})_{f,V} = \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} – \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} (열역학 1법칙에서 파생된 식)
첫 번째 항인 \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} 은
Metal 과 관련이 있다고 할 수 있고,
두 번째 항인 – \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} 은
Polymer 와 관련이 있다고 할 수 있습니다.
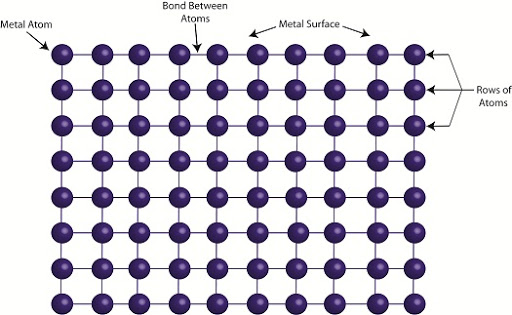
아시다시피
금속은 금속 원자들이 격자 형태로 구조를 이루고 있습니다.
이 원자들은 자유전자에 의해 구속되어있기 때문에
움직임에 많은 제약이 따릅니다.
열을 받으면
에너지가 생기기 때문에
원자들도 열을 받으면 그 활발한 정도가 증가하겠죠?
그렇지만 금속 원자들의 경우
구속되어 있기 때문에
활발한 정도는 증가할 수 있지만
많은 변위값을 가지지는 못합니다.
즉,
내부에너지는 온도가 올라감에 따라 증가할 수 있지만,
엔트로피는 온도에 따라 큰 변화가 생기지는 못합니다.
(갑자기 엔트로피 개념이 나와서 어려우시죠? 조금만 참아주세요!)
그렇기 때문에 결론적으로
금속의 경우는
첫 번째 항이 \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V}
열역학 1법칙을 주도하는 항이라고 할 수 있습니다.

반대로 폴리머는 어떨까요?
플라스틱과 같은 고분자의 경우
분자구조 덩어리가 길게 연속적으로 공유결합을 하고 있어
마치 국수 가락과 같은 형태로 존재합니다.
아까 살펴봤던 금속원자와는 달리
국수 가락과 국수 가락 사이는
공유결합 또는 금속결합과 같은
강력학 구속조건이 존재하지 않습니다.
기껐해야 electrostatic force 또는 van-der Waals 정도 작용할 뿐이죠.
이 말은
polymer chain (국수 가락) 끼리는 서로의 움직임에 제약이 크지 않기 때문에
열을 받는 상황에서
분자구조 자체의 내부에너지도 증가하겠지만,
금속에 비해 상대적으로 큰 변위값을 갖게될 수 있다는 뜻입니다.
엔트로피는
쉽게 말해 무질서함의 척도라고 할 수 있는데요.
경우의 수가 많으면 많을수록 무질서도가 커지게 됩니다.
포커를 예로 들 때
원페어보다
풀하우스가 나오기 더 힘들죠?
원페어가 좀더 엔트로피가 크다고 할 수 있는거죠.
같은 카드를 갖고 좀더 많은 경우의 수로 만들어낼 수 있기 때문이니까요.
이 세상은 엔트로피가 증가하는 방향으로 움직이고 있기 때문에 (열역학 2법칙)
엔트로피가 큰 경우(원페어)가 일반적일 것이고,
엔트로피가 작은 경우(풀하우스)는 매우 드물테니까
풀하우스가 원페어를 이기는 건
꽤 괜찮은 규칙인 것 같습니다.
다시 돌아가서
플라스틱에 열을 가하는 상황을 생각해보면,
온도가 증가함에 따라
국수 가락과 같은 polymer chain 들이
에너지가 증가하게 되고,
국수가락들이 더 활발하게 움직일 수 있게 되며,
좀더 다양한 경우의 수로 공간을 채울 수 있다는 뜻이 됩니다.
즉, 온도가 증가함에 따라 엔트로피가 증가한다는 뜻이죠.
그렇기 때문에
플라스틱의 경우
두 번째 항이 \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V}
열역학 1법칙을 주도하는 항이라 할 수 있겠습니다.

(\frac{\partial{l}}{\partial{T}})_{f,V} = \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} – \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} (열역학 1법칙에서 파생된 식)
금속의 경우는
첫 번째 항인
\frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} 가
열역학 1법칙을 주도하는 항이라고 할 수 있다고 말씀드렸습니다.
두 번째 항을 무시할 수 있다고 하면
(\frac{\partial{l}}{\partial{T}})_{f,V} = \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} (금속의 경우)
가 될 수 있겠습니다.
그리고
온도가 증가함에 따라
내부에너지가 증가하기 때문에
(\frac{\partial{l}}{\partial{T}})_{f,V} 의 값은 양수가 되어
팽창한다는 결론에 도달할 수 있습니다.

(\frac{\partial{l}}{\partial{T}})_{f,V} = \frac{1}{f} (\frac{\partial{U}}{\partial{T}})_{f,V} – \frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} (열역학 1법칙에서 파생된 식)
유사하게
플라스틱의 경우는
두 번째 항인
\frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} 가
열역학 1법칙을 주도하기 때문에
첫 번째 항을 무시할 수 있다고 한다면
(\frac{\partial{l}}{\partial{T}})_{f,V} = -\frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} (플라스틱의 경우)
가 될 수 있습니다.
그리고 결국
온도가 증가함에 따라
엔트로피가 증가하기 때문에
\frac{T}{f} (\frac{\partial{S}}{\partial{T}})_{f,V} 의 값은 양수가 되는데
앞에 마이너스 부호가 있기 때문에
오히려 (\frac{\partial{l}}{\partial{T}})_{f,V} <0 이 되어
수축한다는 사실을 알 수 있습니다.
정리하면,
- 금속은 열을 받으면 팽창
- 플라스틱은 열을 받으면 수축
인데요.
고무줄은 플라스틱에 속하고,
열을 받으면 수축한다는 말은
반대로 얘기하면
팽창하면 열은 방출한다가 되기 때문에
처음에 했던 질문인
왜 고무줄은 잡아 당겼을 때 열을 방출할까?
에 대한
답이 될 수 있겠습니다.
역학을 제대로 이해하면
물리적인 현상을 보는 관점이 바뀌고
간단한 사실이지만
매우 흥미롭게 즐길 수 있습니다.
이런 폴리머 또는 금속의 열특성은
3D printer 의 설계
또는
많은 device 의 공학적 디자인에서 매우 중요합니다.
열역학의 기본 개념과
재료학적 개념을
잘 아신다면
훗날 현업에서 문제를 근본적으로 해결할 수 있으실 겁니다.
열심히 공부하시길 바랍니다.