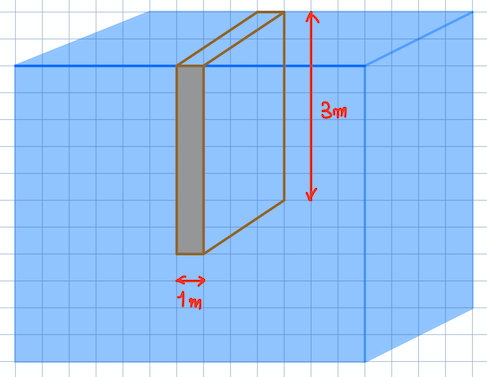
현재 10강 전압력을 듣고 있습니다. 강의를 듣다가 문든 궁금한 점이 생겨서 풀어봤는데 맞는지 확인 부탁드립니다.
10강의 첫번째 문제를 보면 yf(작용점의 위치)를 구하는데 제가 생각하기에는 F=h에 관련된 함수이므로 리니어 하게 증가합니다. 즉 판이 수면에서 시작하면 시작점이 0이므로 전압력의 분포가 삼각형이 됩니다. 마치 분포하중이 삼각형인 형태로 생각할 수 있습니다. 따라서 작용점의 위치는 판의 2/3지점이라고 생각 할 수 있습니다. 그리고 두번째 문제는 수면에서 시작하지 않으므로 사다리꼴의 형태로 전압력이 분포하게 되는데 이는 사다리꼴의 도심을 구하면 됩니다. 즉 h(a+2b)/3(a+b)를 쓰면 됩니다. a와 b는 비중량*높이로 구할 수 있습니다. 따라서 전압력의 작용점 위치는 전압력이 분포하는 도형의 무게중심을 구하는것과 같다고 볼 수 있습니다. 따라서 Ay=인테그랄ydA를 써서 작용점의 위치를 구할 수 있다고 생각이 듭니다. 제 생각이 맞는건가요??? 고체역학을 공부하고 듣다보니 고체역학의 분포하중을 구하는 방법으로 구해도 된다는 생각이 들어서 문의드립니다.
그럼 판이 수면으로 떨어져 있다는 가정하에 사다리꼴의 도심의 공식을 이용하면 작용점의 위치는 =판의 길이(수면으로부터 가장 가까운 높이2+수면으로 부터 가장 먼 높이)/3(수면으로부터 가장 가까운 높이+수면으로 부터 가장 먼 높이) 라는 아주 간단한 공식이 완성됩니다. 단 이 위치는 판의 가장 먼곳에서부터 도심까지의 거리이므로 가장깊은곳까지의 거리에서 저 값을 빼면 Fy값이 나옵니다. 맞는지 궁금합니다.
답변
말씀하신 게 정확히 맞습니다.
그렇게 구하셔도 됩니다.
사실 전압력이라는 것이 그렇게 특별한 것은 아닙니다.
유체의 비중에 의해서 유체에 의한 압력이 발생되고,
이런 물리적 현상에 따른 물체의 거동을 보는 것이기 때문에
고체역학에서 배운대로
어떤 가상의 삼각형 또는 사다리꼴 형태의 분포하중이 있다고 가정하고
이에 대한 도심으로 구하는 것은 전혀 문제될 것이 없겠습니다.
아래와 같이 작용점의 위치 공식을 이용해서 구하나
삼각형의 도심을 이용하나
같은 것을 확인하실 수 있겠습니다.
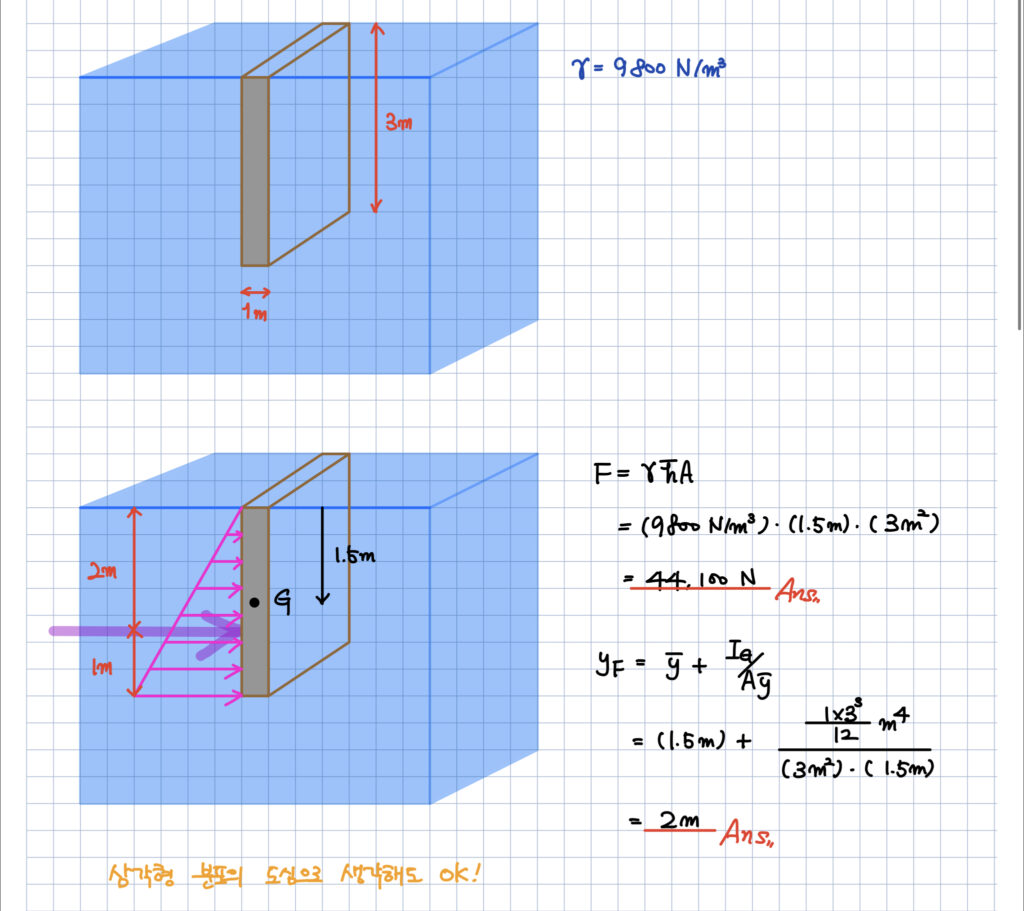
또한 말씀하신 것처럼
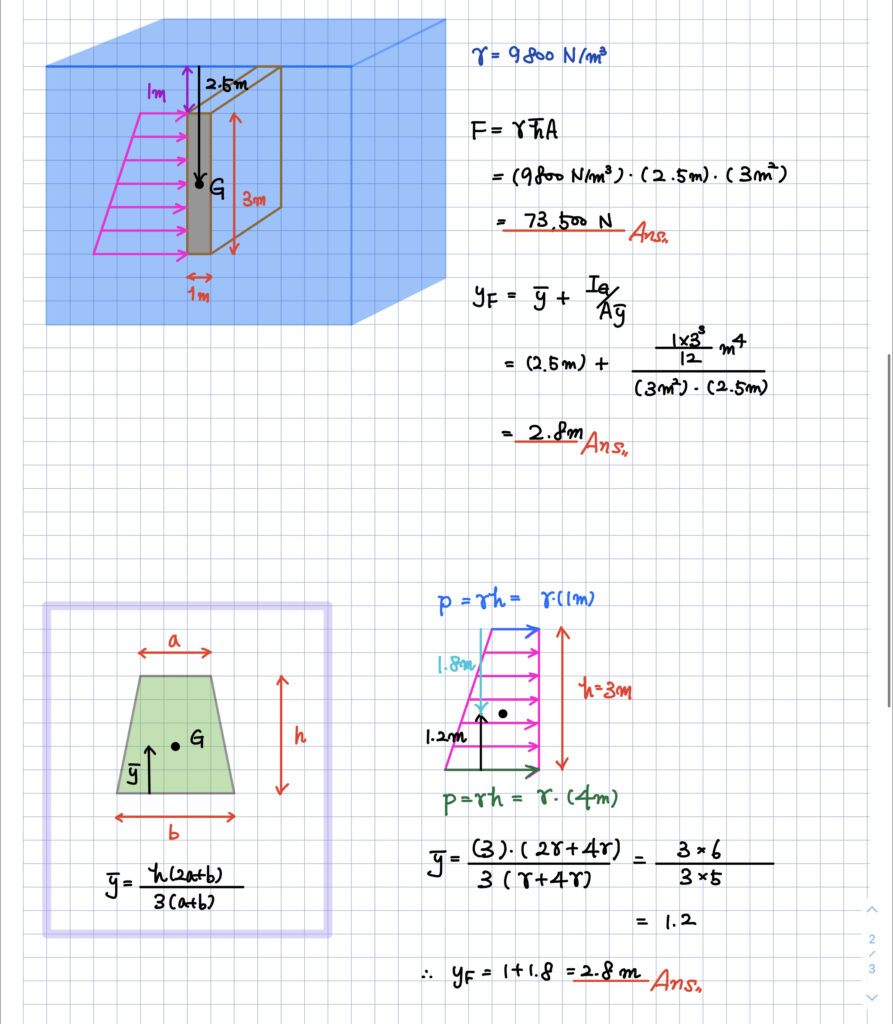
사다리꼴의 도심을 이용해도 아래와 같이 구할 수 있겠습니다.
첫 번째는 작용점의 위치 공식을 이용해서 구한 것이고
두 번째는 사다리꼴의 도심 공식을 이용해서 구한 것인데
둘 다 값이 똑같다는 것을 확인하실 수 있습니다.
혹시라도
유체에 수직으로 잠겨있는 물체에
왜 삼각형 또는 사다리꼴로 분포하중이 가해지는지 모르시는 학생분이 계신다면
아래의 링크를 통해 복습해보시길 바랍니다.
액체 속에 잠긴 수직 평면인 경우, 왜 압력 분포는 삼각형 형태로 되어 있나요?
마지막엔 학생분께서 어떤 공식처럼 만들어서 사용하시려고 하셨는데
그렇게 쓰셔도 괜찮지만
사실 저는 공식을 외우는 것을 지양하는 편이라
별로 공식을 외울 것을 추천하지는 않습니다.
사실 사다리꼴의 도심도 외우기 꽤 벅찬 식이고,
차라리 삼각형+사각형으로 나눠서 도심을 계산하는 편이 더 쉬운 것 같고 이를 추천하는 편입니다.
작용점의 공식도 사실 유도할 줄만 알면
외우지 않아도 충분히 알 수 있는 것이라
작용점의 위치 정도는 공식을 이용해서 푸는 것이 좋겠으나
따로 공식을 굳이 만들어야하나… 생각이 들긴 합니다.
물론 학생분이 편하다고 생각되고,
빠른 시간 내에 많은 문제를 풀어야 하는 상황이 생긴다면,
그러한 방법도 괜찮을 수 있습니다.
하지만 보통 수직으로 잠겨있는 물체보다는
각도를 가지고 비스듬하게 잠겨있는 경우가 많이 나오기도 하기 때문에
항상 공식을 외우기 보다는
governing equation을 바탕으로
유도하여 원하는 값을 구하는 방법으로 연습할 것을 추천드립니다.
물론 학생분께서 질문 주신 것과 같이
고체역학의 개념을
유체역학과 연결하여 이해하려고 하신 시도는
매우 좋고 바람직하다고 생각합니다.
좋은 질문 해주셔서 감사합니다.
항상 이런 식으로 유연하고 다양하게 고민해보고 공부해보시길 바랍니다.
감사합니다.