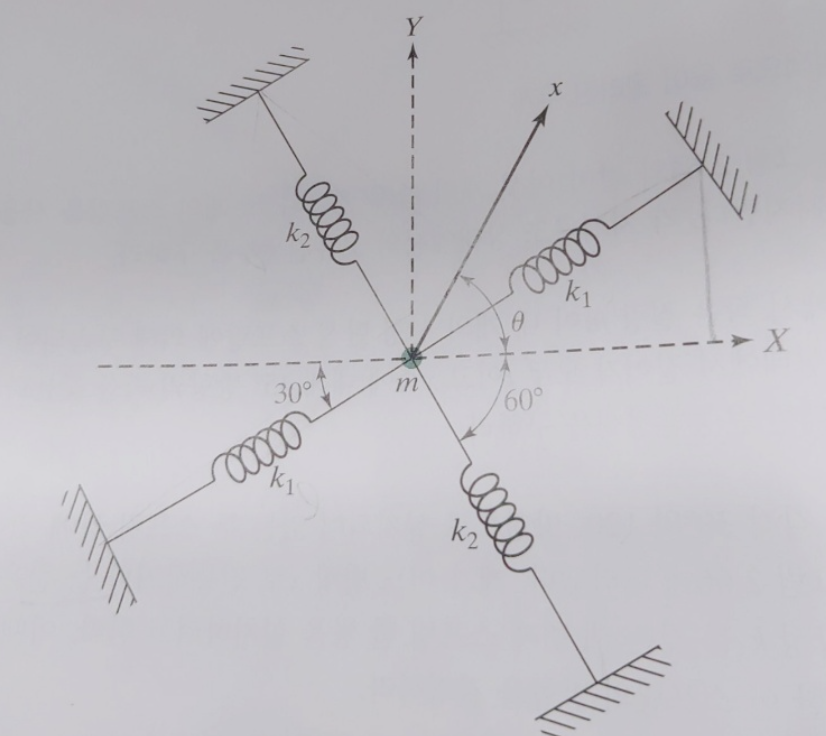
#기계진동학질문 #고유진동수
아래문제를 풀때 x방향에 상관없이 고유진동수가 일정하다는 문제의 조건을 이용해서, 고유진동수 식 내부에 x방향을 가르키는 theta항이 없어야하는거 아닌가요?? 식을세웠는데 풀이에 진전이없네요 ㅜㅜ

답변
이 문제는 어려운 건 아닌데,
기본이 안 잡혀있으면 손을 못 댈 수도 있는 문제입니다.
약간의 계산 능력도 필요하구요.
“각도에 상관없이”라는 말을 보면서 각도에 대한 함수로써 표현한 후
계수를 0으로 해야 한다는 센스도 조금 있으셔야 합니다.
어쨌든 비교적 어려운 문제인데요.
이런 문제들 때문에
단순히 공식을 외워서 문제를 풀지 말라고 제가 조언드리는 겁니다.
제가 항상 강조하는
원리/원칙/기본개념에 충실한다면
어떤 문제가 나와도 아주 쉽게 접근하실 수 있으실 겁니다.
바로 이 문제를 풀기 전에
우리 비슷한 문제부터 풀면서
개념에 대한 이해를 해보도록 합시다.
아래와 같이 삼각형 형태로 구성된 스프링 세트에서
질량 m을 y방향으로 진동시켰을 때의 고유진동수를 구해봅시다.
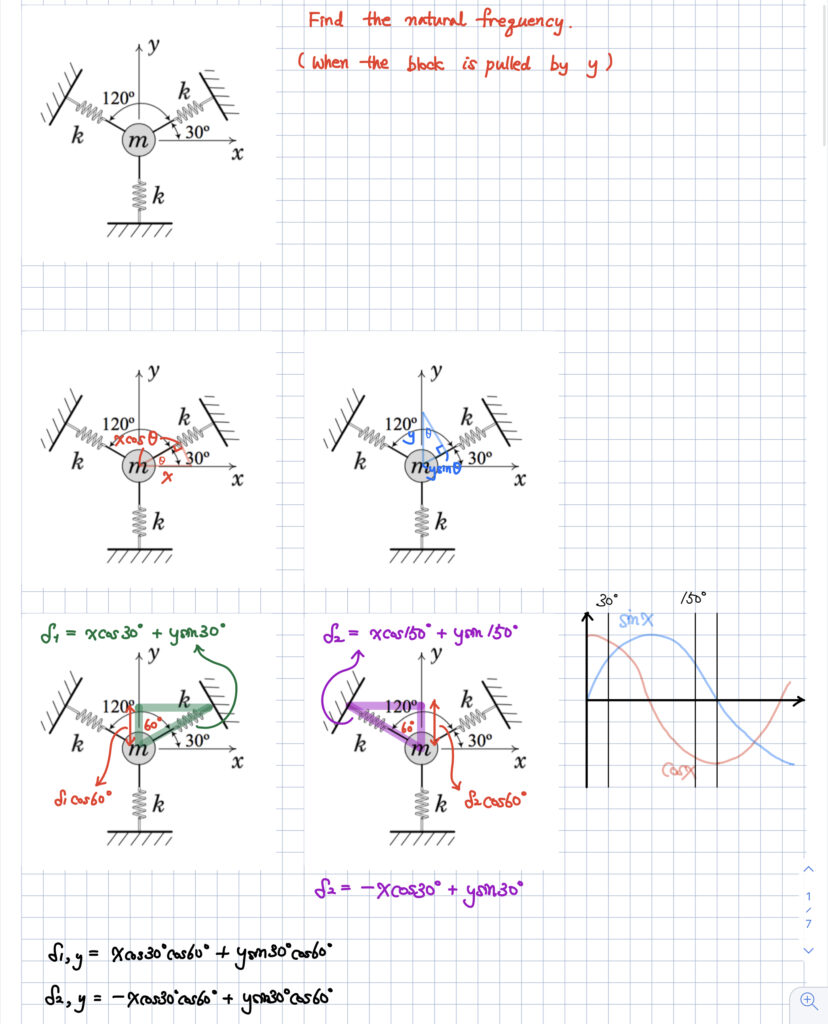
이 문제의 핵심은
해당 방향으로의 displacement 및 force를 계산하여
equivalent spring stiffness를 계산하는 것이 핵심입니다.
등가 강성만 구할 수 있다면 고유진동수는 아주 쉽게 계산할 수 있겠습니다.
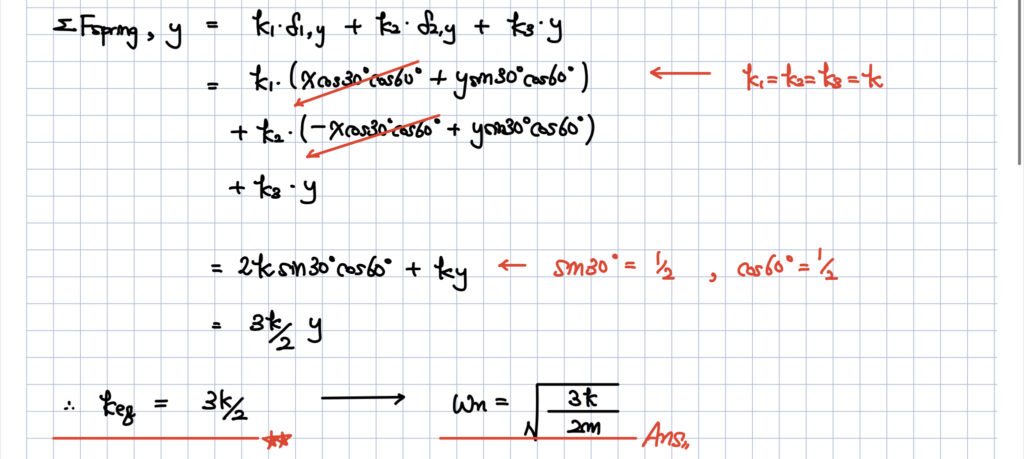
조금만 문제를 업그레이드 해보죠.
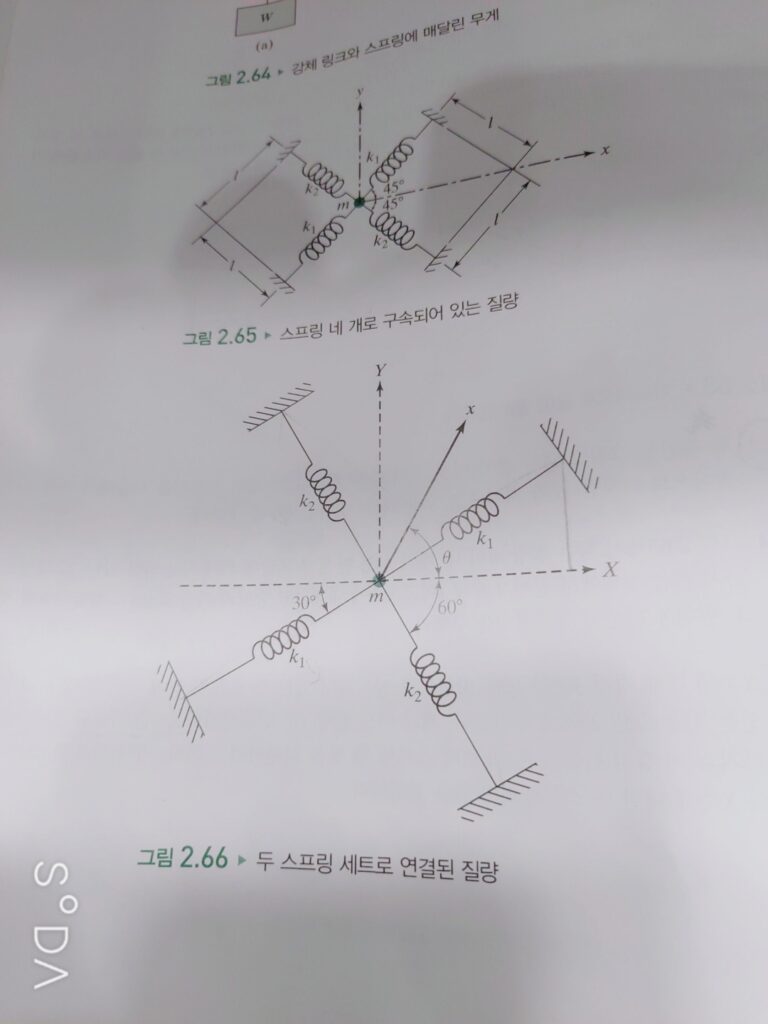
아래와 같이 구성된 물체에서
이번엔 x방향으로 진동을 시켰을 때 고유진동수를 구해보도록 합시다.
첫 번째 문제에서 구한 내용을 잘 이해하셨다면
equivalent stiffness를 어느 방향에서든지 쉽게 계산할 수 있겠습니다.
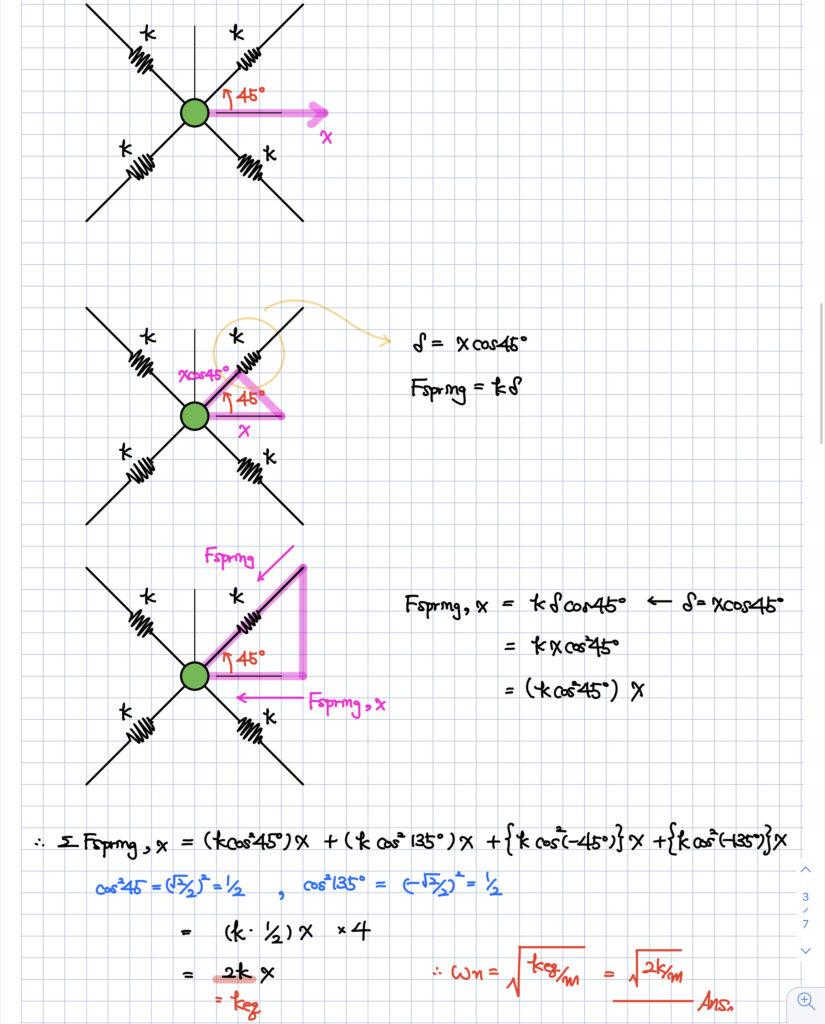
절대로 공식을 외워서 풀지 마세요!
\Sigma F_x = k x cos^2\alpha뭐 이런 식으로 cos 제곱하고 이런 식으로 식을 외워서 푸는 분이 많던데,
결국 이렇게 연습하면
원래 질문했던 문제와 같이 조금이라도 복잡해지면 식을 어떻게 적용해야할지 모르는 상황이 발생합니다.
반드시 기본에 충실하여 공부하시길 바랍니다.
자, 이제 질문했던 문제를 풀어보도록 합시다.
조금은 복잡하지만 위의 내용을 이해할 수 있었다면 잘 해결하실 수 있으실 겁니다.
각 스프링 요소대로 x 방향에 작용하는 힘을 천천히 계산해줍니다.
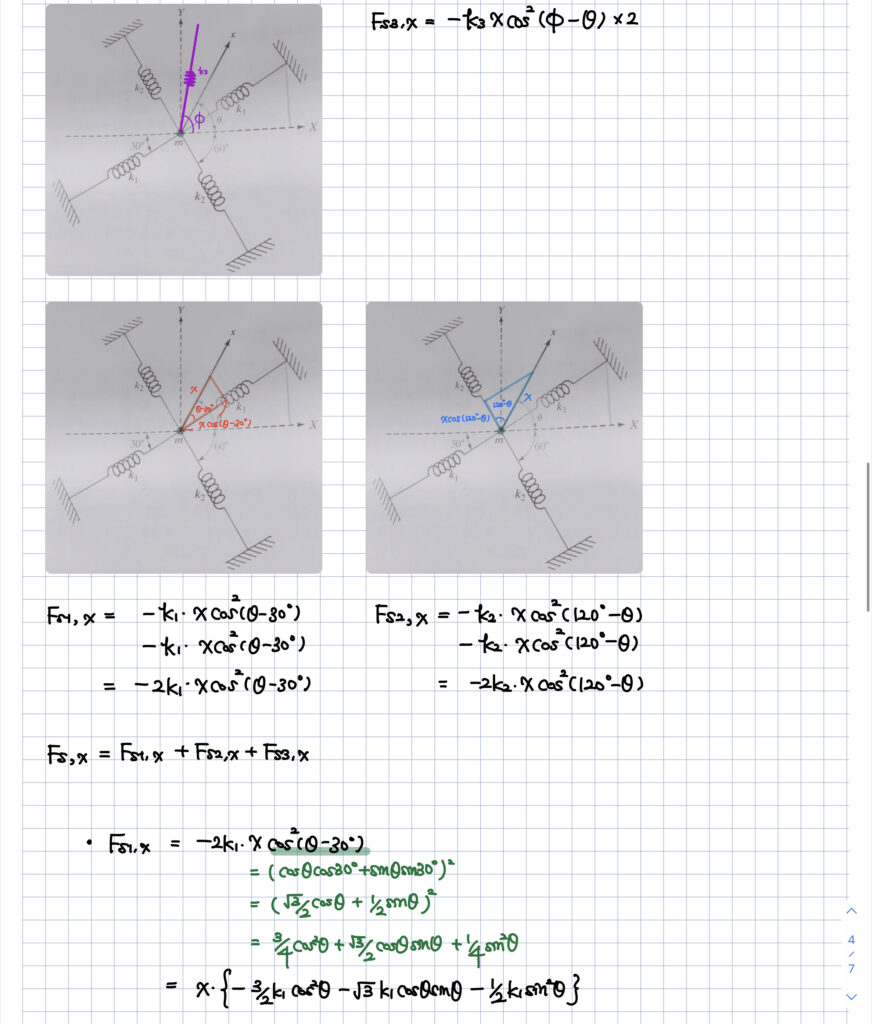

이 문제에서의 핵심은
\theta에 independent한 equivalent stiffness를 구하는 것이기 때문에
이 성질을 이용해서 식을 계산해주면 되겠습니다.
조금 수학적으로 궁금할 수 있는 예상되는 질문은…
왜 cos^2\theta 와 cos\theta sin\theta 를 굳이 나눠서 계수 처리를 하냐는 질문일 수 있는데,
비선형 방정식이기 때문에
제곱의 항과 일반 항은 엄연히 다른 성격을 가지고 있기 때문에
따로 묶어줘서 계수를 0으로 처리를 해줘야 하겠습니다.
모르는 항 2개
풀 수 있는 식 2개 이기 때문에
풀 수 있는 방정식이 되고
아래와 같이 풀이를 마칠 수 있겠습니다.

다시 한번 강조하지만,
진동학은 더더욱
절대 공식을 외워서 풀지 마세요.
시간을 낭비하는 길입니다.
제가 위에서 풀었던 것처럼
FBD를 바탕으로
천천히 기본 개념을 이용해서 계산하시면
어떤 응용문제도 푸실 수 있을 거라 확신합니다.
질문에 대한 답이 됐기를 바랍니다.
감사합니다.