
[(New) 유체역학 퍼펙트 완성] 16강 (3번 예제) 50:10
Author
갓준표
Date
2024-10-13 07:01
Views
501
교수님 안녕하세요!
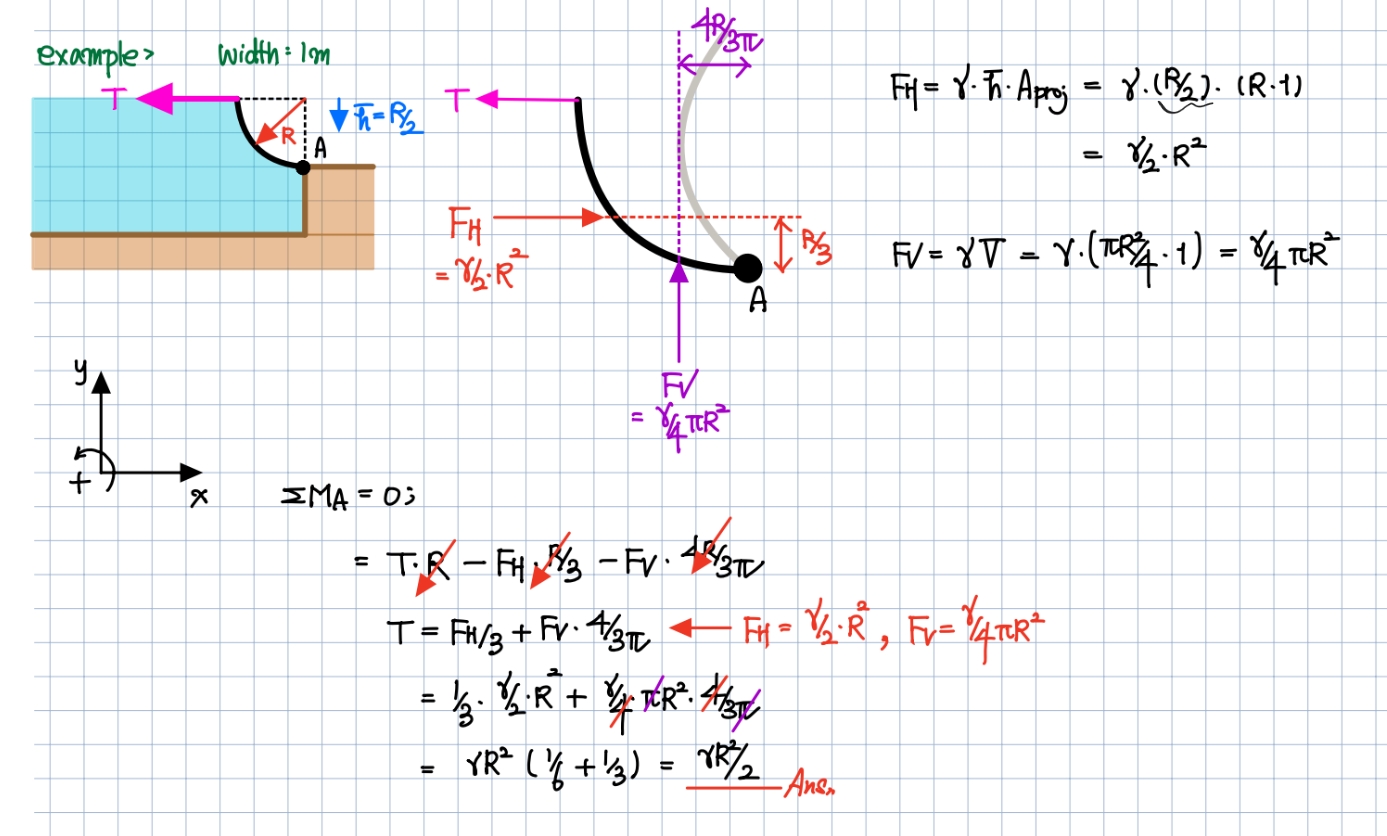
16강 50:10 즈음 (3번 예제) 총힘의 수직성분은 곡면의 압력중심에 작용하는 것으로 생각하고 수평성분은 정사시킨 면의 압력중심에 작용하는 것으로 생각해야 한다고 하셨습니다. 어떠한 차이때문에 두 상황을 다르게 봐야하는지가 궁금합니다.
감사합니다!
#유체역학 #곡면 압력 중심 #전압력
16강 50:10 즈음 (3번 예제) 총힘의 수직성분은 곡면의 압력중심에 작용하는 것으로 생각하고 수평성분은 정사시킨 면의 압력중심에 작용하는 것으로 생각해야 한다고 하셨습니다. 어떠한 차이때문에 두 상황을 다르게 봐야하는지가 궁금합니다.
감사합니다!

#유체역학 #곡면 압력 중심 #전압력
Fluid Mechanics, M. White, McGrawHill
Ch. 1 Introduction
Ch. 2 Pressure Distribution in a Fluid
Ch. 3 Integral Relations for a Control Volume
Ch. 4 Differential Relations for Fluid Flow
Ch. 5 Dimensional Analysis and Similarity
Ch. 6 Viscous Flow in Ducts
Ch. 7 Flow Past Immersed Bodies
Ch. 8 Potential Flow and Computational Fluid Dynamics
Ch. 9 Compressible Flow
Ch. 10 Open-Channel Flow
Ch. 11 Turbomachinery
- “유체역학 한방에 끝내기” 는 초등학생도 이해할 수 있게끔 쉽고 재미있게 유체역학을 설명하고 있습니다.
- 공식만 외워서 문제를 푸는 방식은 올바른 역학 공부법이 아니고, 조금만 응용된 문제가 나오면 접근하기가 매우 어려워져 좋은 시험 점수(좋은 학점)을 받기가 매우 어려워집니다.
- 원리와 원칙에 충실하여 어떤 문제가 나와도 개념에 충실해서 풀 수 있어야 학업성취도, 취업 면접, 대학원 시험 등에서 좋은 결과를 기대할 수 있습니다.
곡면에 작용하는 전압력 및 그 작용점에 대한 설명으로는 제 강의와 아래의 설명으로 충분히 이해가 되실 겁니다. 질문하신 내용을 그대로 적으면 아래와 같습니다.
- 수직성분은 왜 곡면의 압력중심이고
- 수평성분은 왜 정사면의 압력중심이냐
그러나 저는 그렇게 설명드렸다기 보다는 곡면의 경우 정사면으로 고려해 줘야 한다는 것을 강조했던 것으로 기억합니다. (혹시라도 오해가 있었다면 죄송합니다.)
제가 질문에 대한 이해가 조금 부족한데, 아래의 설명을 참고하셔서 추가로 질문이 있다면 제게 다시 해주시기 바랍니다. 열심히 공부해 주셔서 정말 감사합니다!
[곡면에 작용하는 전압력 관련 답변]
곡면에 작용하는 전압력과 그 성분들의 작용점에 대해 자세히 설명해 드리겠습니다.
전압력의 개념:
곡면에 작용하는 전압력은 유체가 곡면 전체에 가하는 모든 힘의 합력입니다. 이는 수직 성분과 수평 성분으로 나눌 수 있습니다.
전압력의 작용점:
전압력의 작용점은 압력중심이라고 하며, 이는 곡면의 형상과 압력 분포에 따라 결정됩니다.
수직 성분과 수평 성분의 차이:
a) 수직 성분:
수직 성분은 곡면의 실제 형상을 고려하여 계산됩니다.
압력 중심은 곡면의 실제 형상 상에 위치합니다.
이는 곡면의 기하학적 특성과 압력 분포를 모두 반영합니다.
b) 수평 성분:
수평 성분은 곡면을 수직 평면에 투영한 면적에 대해 계산됩니다.
압력 중심은 이 투영된 평면 상에 위치합니다.
이는 실제 곡면의 형상보다는 투영된 면적의 특성을 반영합니다.
차이가 발생하는 이유:
a) 기하학적 차이:
곡면의 실제 형상과 투영된 형상은 다릅니다.
수직 성분은 실제 곡률을 고려하지만, 수평 성분은 평면화된 형상을 다룹니다.
b) 압력 분포의 차이:
수직 방향으로의 압력 변화는 깊이에 따라 선형적이지만, 수평 방향으로는 복잡한 분포를 가질 수 있습니다.
c) 힘의 작용 방향:
수직 성분은 곡면의 법선 방향으로 작용하지만, 수평 성분은 투영 평면에 평행하게 작용합니다.
실제적인 의미:
이러한 차이는 구조물 설계나 유체 시스템 분석에서 중요합니다.
예를 들어, 댐이나 선박의 곡면 설계 시 이러한 차이를 고려해야 정확한 힘의 분포와 작용점을 파악할 수 있습니다.
계산의 편의성:
수평 성분을 투영 면적에 대해 계산하는 것은 복잡한 3차원 계산을 단순화하여 문제 해결을 용이하게 합니다.
결론적으로, 곡면에서의 전압력 계산에서 수직 성분과 수평 성분을 다르게 다루는 것은 실제 물리적 상황을 더 정확히 반영하면서도 계산의 효율성을 높이기 위한 접근 방법입니다. 이는 유체역학 문제 해결에 있어 중요한 개념적 토대를 제공합니다.