
카테고리: 원하는 부분만 골라! 골라!
순서: 남들이 많이 봤던 내용들만 먼저! 먼저!
키워드 검색: 원하는 내용만 뽑아! 뽑아!
[동역학 24강] 예제 4.6번 surface2 공식 관련 질문입니다.
Ch. 4 Kinetics of Systems of Particles
작성자
갓준표
작성일
2024-11-30 08:34
조회
92
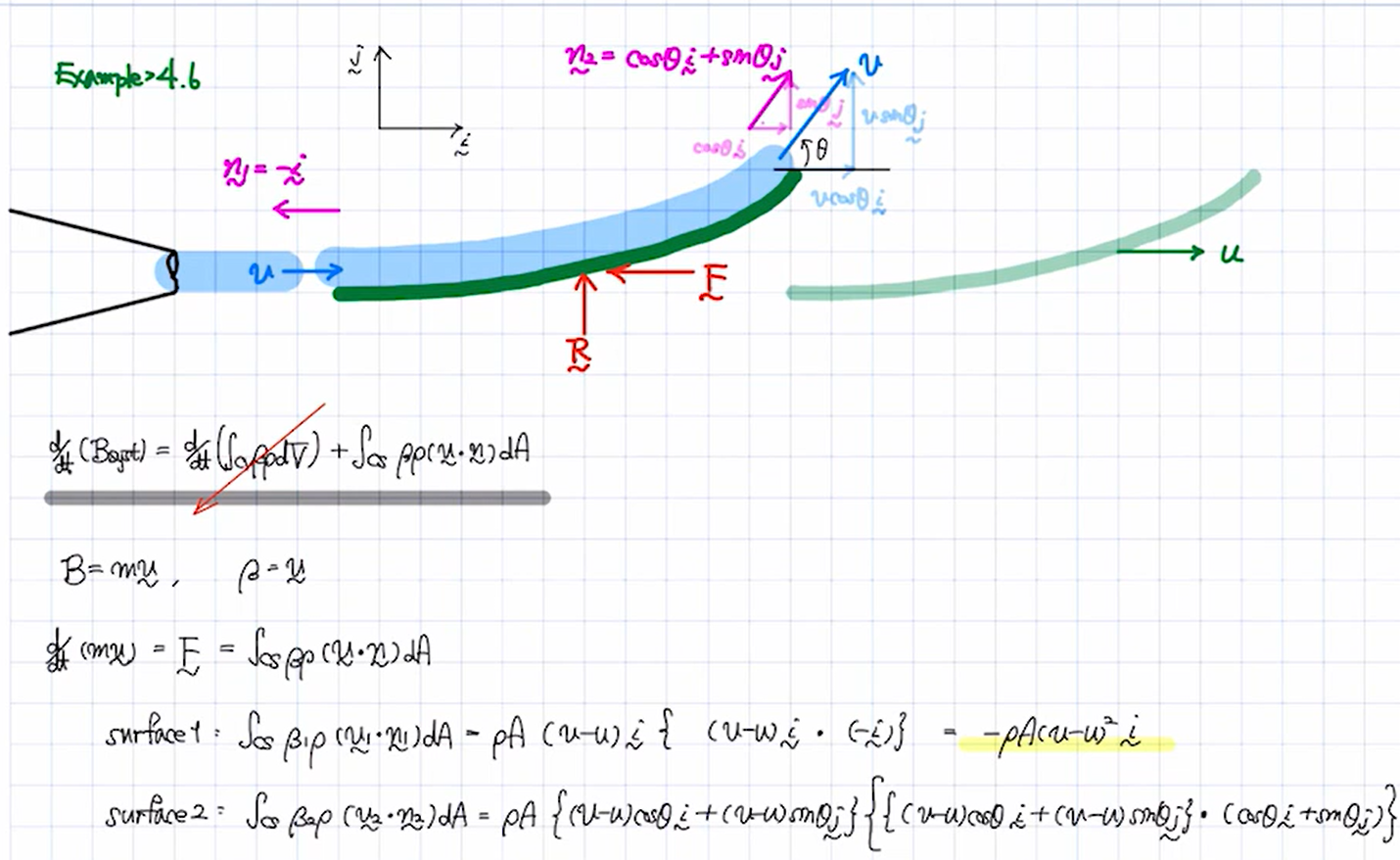
surface 2에서 v2를 구할때 (v-u)를 이용하여 구했는데 v2가 v-u인 것까지는 알겠습니다. 하지만 이를 i-j성분으로 나누어 식을 전개할때
u의 경우 j성분은 존재하지 않고 i성분만 존재하므로
v2가 (v-u)cos(θ)i+(v-u)sinθj가 아니라 (vcosθ-u)i+vsinθ가 되어야하는것 아닌가요?
왜 usinθj term 이 존재하는지 궁금합니다
또한 만약 u가 i성분만 존재하는 벡터가 아니라 임의의 벡터라고 하더라도 u가 가지는 각도가 θ가 아니라 다른 값일텐데
왜 (v-u)cos(θ)i+(v-u_sinθj로 u도 sin θ와 cos θ로 분해하여 다음과 같은 공식이 나왔는지 모르겠습니다.
벡터의 뺄셈을 이용한 상대속도와 이를 성분을 나눠 빼는 것이 혼합되어 공식 부분이 잘 이해되지 않고 헷갈리네요..
#레이놀즈 수송정리 #예제풀이 #벡터성분분해
u의 경우 j성분은 존재하지 않고 i성분만 존재하므로
v2가 (v-u)cos(θ)i+(v-u)sinθj가 아니라 (vcosθ-u)i+vsinθ가 되어야하는것 아닌가요?
왜 usinθj term 이 존재하는지 궁금합니다
또한 만약 u가 i성분만 존재하는 벡터가 아니라 임의의 벡터라고 하더라도 u가 가지는 각도가 θ가 아니라 다른 값일텐데
왜 (v-u)cos(θ)i+(v-u_sinθj로 u도 sin θ와 cos θ로 분해하여 다음과 같은 공식이 나왔는지 모르겠습니다.
벡터의 뺄셈을 이용한 상대속도와 이를 성분을 나눠 빼는 것이 혼합되어 공식 부분이 잘 이해되지 않고 헷갈리네요..
#레이놀즈 수송정리 #예제풀이 #벡터성분분해

Engineering Mechanics: Dynamics, James L. Meriam, L. G. Kraige, Willey
Part I Dynamics of Particles
Ch. 1 Introduction to Dynamics
Ch. 2 Kinematics of Particles
Ch. 3 Kinetics of Particles
Ch. 4 Kinetics of Systems of Particles
Part II Dynamics of Rigid Bodies
Ch. 5 Plane Kinematics of Rigid Bodies
Ch. 6 Plane Kinetics of Rigid Bodies
Ch. 7 Introduction to Three-Dimensional Dynamics of Rigid Bodies
Ch. 8 Vibration and Time Response
- “동역학 한방에 끝내기” 는 초등학생도 이해할 수 있게끔 쉽고 재미있게 동역학을 설명하고 있습니다.
- 공식만 외워서 문제를 푸는 방식은 올바른 역학 공부법이 아니고, 조금만 응용된 문제가 나오면 접근하기가 매우 어려워져 좋은 시험 점수(좋은 학점)을 받기가 매우 어려워집니다.
- 원리와 원칙에 충실하여 어떤 문제가 나와도 개념에 충실해서 풀 수 있어야 학업성취도, 취업 면접, 대학원 시험 등에서 좋은 결과를 기대할 수 있습니다.
안녕하세요.
지적해주신 부분이 정확히 맞습니다.
그림에 대한 설명이 있어야 했는데 부족했던 것 같습니다.
원래 문제에서는
v 대신 v-u로 표시되어 있습니다.
그래서 첨부된 사진처럼 v-u로 바뀌어야 합니다.
정리하자면,
v가 아닌 v-u라고 쓰든가
아니면 방향을 살짝 바꿔서 v'라고 다시 정의를 했어야 합니다.
나머지 풀이에서는 문제가 없습니다.
추가로 궁금한 부분이 있다면 알려주세요.
좋은 질문해 주셔서 감사합니다.