질문
안녕하세요 한.끝 고체 모두 완강했습니다! 너무 잘 들었고 도움이 많이 되었습니다
제가 생각하는 문제중에 계속해서 이해가 안되는 부분이 있어서 구조요청 해봅니다.
글이 길더라도 확인해주시면 감사하겠습니다.

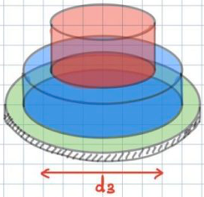
사진의 문제를 보면 최소 d 1,2,3를 구해야 합니다.
A의 (Bearing) Normal Stress는 당연히 Normal internal Force (or P)/Area A 으로 잡고 풀 수 있었습니다.
즉, 350MPa=140 k N/(pi*d1^2/4) 으로 d1값의 후보를 정해볼 수 있습니다.
이제 각 디스크에 FBD를 봐보면
A 읫부분에 아래방향으로 140kN ‘외부하중’이 작용하므로 역학적평형을 만족하기 위해
외부하중과 같은 선상에 ‘A와 B가 맞닿는 부분’에서 B가 A에게 140kN 위방향으로 집중하중을 줄 것입니다
B도 마찬가지 방법으로 A가 B에게 140kN C가 B에게 140kN을 서로 반대방향으로 줄 것입니다.
C도 B가 뻥 뚤려 있는 곳 중간에 집중하중을 줄 것이고
C에 맞닿은 바닥면이C에게 집중수직항력을 줄 것입니다.
이때 C의 면적을 어디로 잡아야 되냐가 문제입니다.
분명 모든 면적에 normal stress가 작용할텐데 C의 Normal stress의 Area가 (전체C면적-지름이 d3인 면적) 이 아니라
(지름이 d2면적-지름이 d3인 면적)을 구해야 됩니다.
사실 저는 A,B,C를 하나의 시스템으로 보고 풀었는데 C에서 부터 막히더군요
Shear Stress도 마찬가지입니다.
단순히 보면 그냥 단면적으로 보면 될 것 같은데
A의 shear stress를 계산하려 했더니 두께가 안나와 있고
B의 shear stress의 Area는 pi*d2*20가 아닌 ‘pi*d3*20’ 로 잡아야되고
C의 shear stress의 Area는 단순하게 pi*d 2*10 으로 잡아야 답이 나옵니다.
이유를 모르겠습니다…
답변
일단 이 문제가 어려워보이는 이유는 디스크들이 어떻게 생겼는지 단면도로는 이해가 좀 안되는 부분이 있습니다. 제가 최대한 이해가 잘 되게끔 풀이를 다시 했으니 살펴보시길 바랍니다.
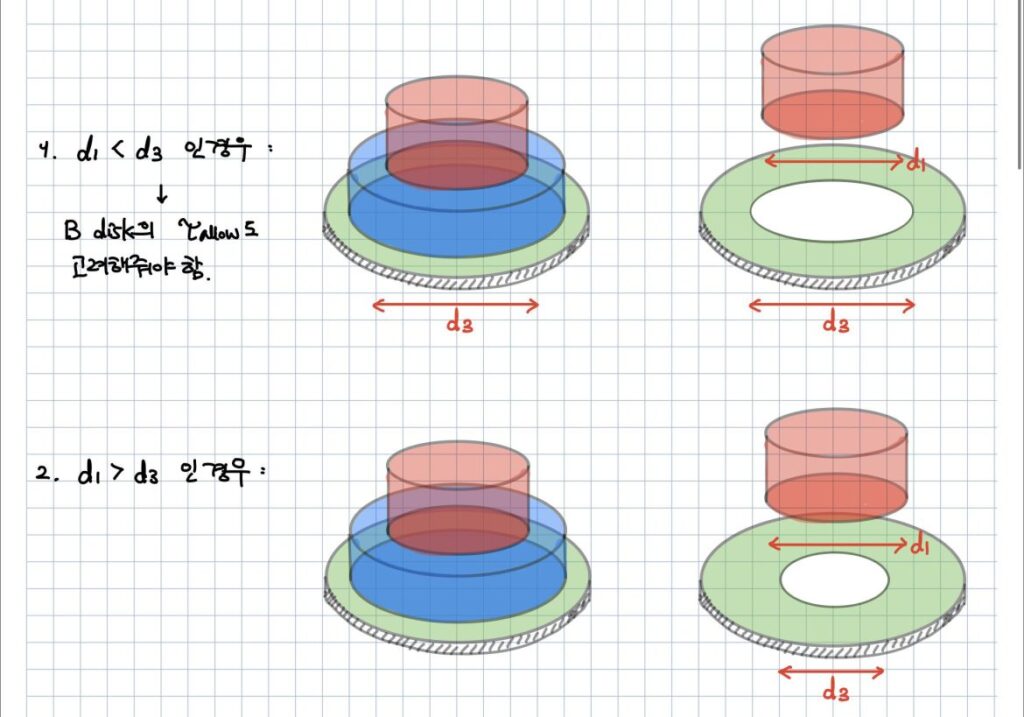
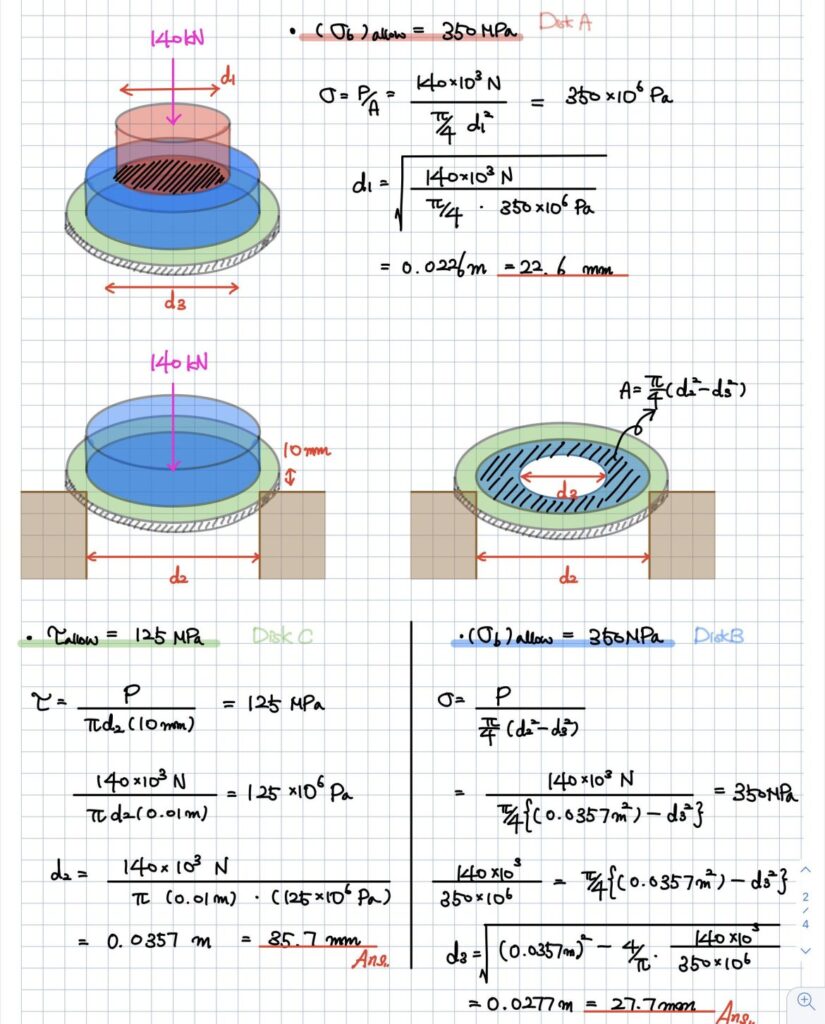
먼저 수직응력으로 d1을 계산하고, d2와 d3를 차례대로 구합니다. (Disk A, B, C 구분이 1차 수정되었습니다.)

d1<d3이기 때문에 혹시 모를 전단응력에 의한 파괴도 고려해서 d1을 다시 확인해봐야 합니다. d3를 계산해봐야 전단응력을 고려해야 하는지 마는지를 결정할 수 있기 때문에 여기서 다시 확인하는 것입니다.
재질문
죄송합니다 지금봤네요. 계속 고민중인데 사실 잘 이해가 안갑니다ㅠㅠ
두번째 사진 수직/전단응력부터 잘 이해가 안갑니다.
꼭은 아니나 보통 bar와 beam형태로 수직 및 전단응력 개념을 공부하는데요,
bar에 경우 집중하중÷수평단면 으로 수직응력을 정의하고
beam에서 집중하중÷수직단면 으로 전단응력을 정의하게 됩니다.
같은생각으로
1) Disk A의 경우
A를 bar로 바꾼다고 가정하면 수직응력은 당연히
[140kN ÷ (pi÷4×d1^2)] 일 것입니다.
전단응력은 beam으로 생각해보면 [140kN ÷ A의 수직단면적]
이 전단응력입니다.
2) Disk B의 경우
B부터 계속헷갈립니다. 분명 검은색 칠된영역이 A와 B가 닿는 영역인건 당연합니다.
그런데 B역시 bar로 생각해보면 검은색영역의 분포된 분포하중을 집중하중으로 치환할수 있고 B의 수평단면은 pi÷4×d1^2 가 아니라
pi÷4×d2^2 이 될 것입니다.
전단응력 역시 B를 beam으로 생각해보면 수직단면 넓이는 pi×d2×20
이게됩니다.
3) Disk C의 경우
C도 마찬가지방법으로 했습니다. 다만 C에는 구멍이 뚤려있으므로
수평단면넓이:
[pi÷4×(c의지름)^2-pi÷4×(d3)^2]
수직단면 넓이:
[pi×c의지름×10-pi×d3의지름×10]
이런식의 메커니즘으로 풀었습니다… 어떤 오류가 있는걸까요??
재질문 답변
1) Disk A의 경우
여기서 중요한 것은 A를 통해 가해지고 있는 힘이 B에 전달된다는 것이고, 이때 B의 단면적은 C에 있는 구멍 때문에 (pi/4*(d2^2-d3^2)) 에만 전달된다는 것입니다. 지금 학생분께서는 Disk B를 기준으로 보시는 것이 아니라 Disk A를 기준으로 보고 계시니 자꾸 헷갈리시는 겁니다.
다시 요약하자면, A에 의해 전달된 힘이 Disk B에 영향을 미치는데, 아래의 구숙되는 부분에 Disk C 구멍이 있기 때문에 유효면적이 줄어든느 것이죠.
3) Disk C의 경우
Disk A에 의해 힘이 전달되고 면적이 있기 때문에 수직응력을 계산해야 하는 것처럼 보이지만, 사실 아래에 구속된 것이 없기 때문에 Disk C에는 수직응력에 대한 영향이 없습니다. 오로지 전단응력만 가해질 뿐이죠. 때문에 Disk C에서 수직응력은 고려되면 안됩니다.
*이러고 보니 제가 두번째 사진에 Disk B라고 써야 했는데 C라고 썼네요. 수정하겠습니다.
힘이 가해지고 있는 것과 아래에 구속되어 반발력이 있는지 없는지에 대한 것을 같이 고민하시면 해결되실 것 같습니다.