카스틸리아노 정리, 델i = 라운드U/라운드Pi 에서 에너지를 압력P로 편미분 해주는데, 문제에 적용되었을 때 압력이 상수로 나오게 되면 미분은 어떻게 하는지 궁금합니다. Castigliano’s theorem 은 deflection of Beam 을 다루는 데에 있어서 매우 중요합니다. 같이 살펴보겠습니다.
답변
고체역학 한 방에 끝내기에서
많이 강조했던 Castigliano’s theorem에 관한 질문이 들어왔습니다.
질문은 P가 상수일 때
strain energy (U) 또는 bending moment (M) 에 대해서
어떻게 미분을 할 수 있느냐는 것인데요.
사실 이 질문은
그 자체로 들으면 그럴 듯 해보이지만,
카스틸리아노 정리를 잘 이해하셨다면 나올 수 없는 질문입니다.
답변을 먼저 드리자면,
비록 하중이 상수값이라고 할지라도
그 하중으로 표현되는 모멘트 또는 에너지 값은 P 에 대한 함수로 항상 표현되기 때문에
상수이든
무언가의 함수이든
전혀 문제 없이 미분될 수 있고,
처짐이 계산될 수 있습니다.
아래와 같이 내용을 복습하면서
다시 한번 같이
Castigliano’s theorem 에 대해서
정리해보도록 합시다.
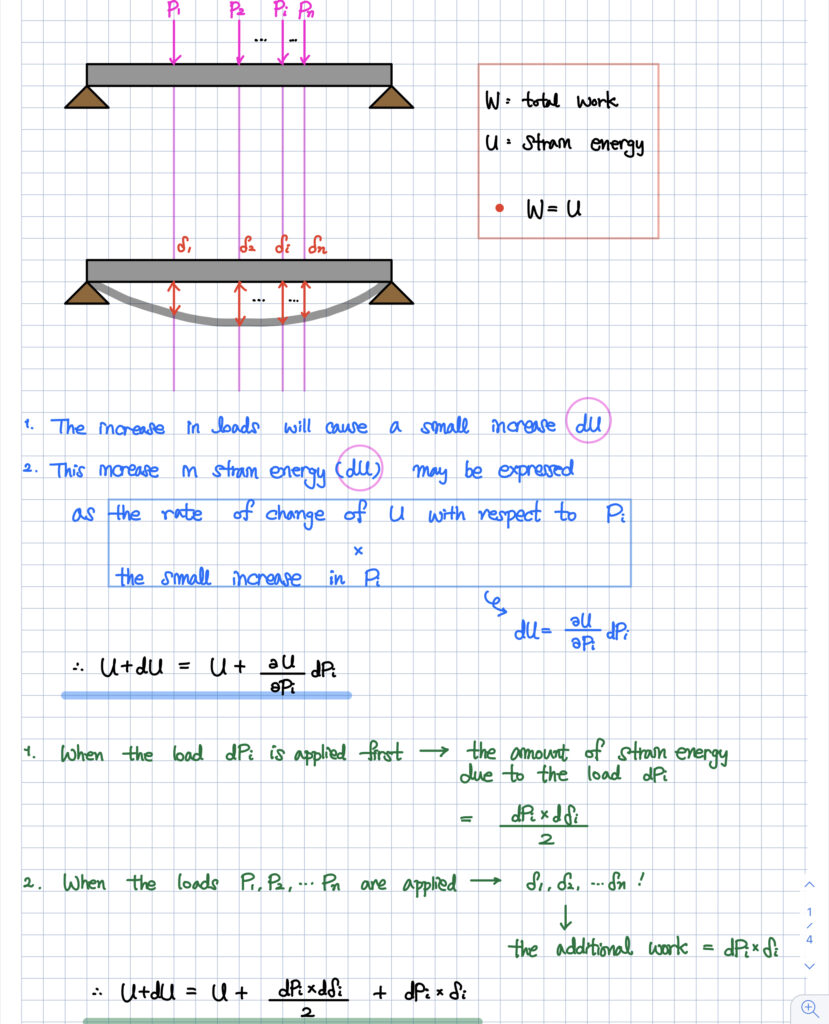
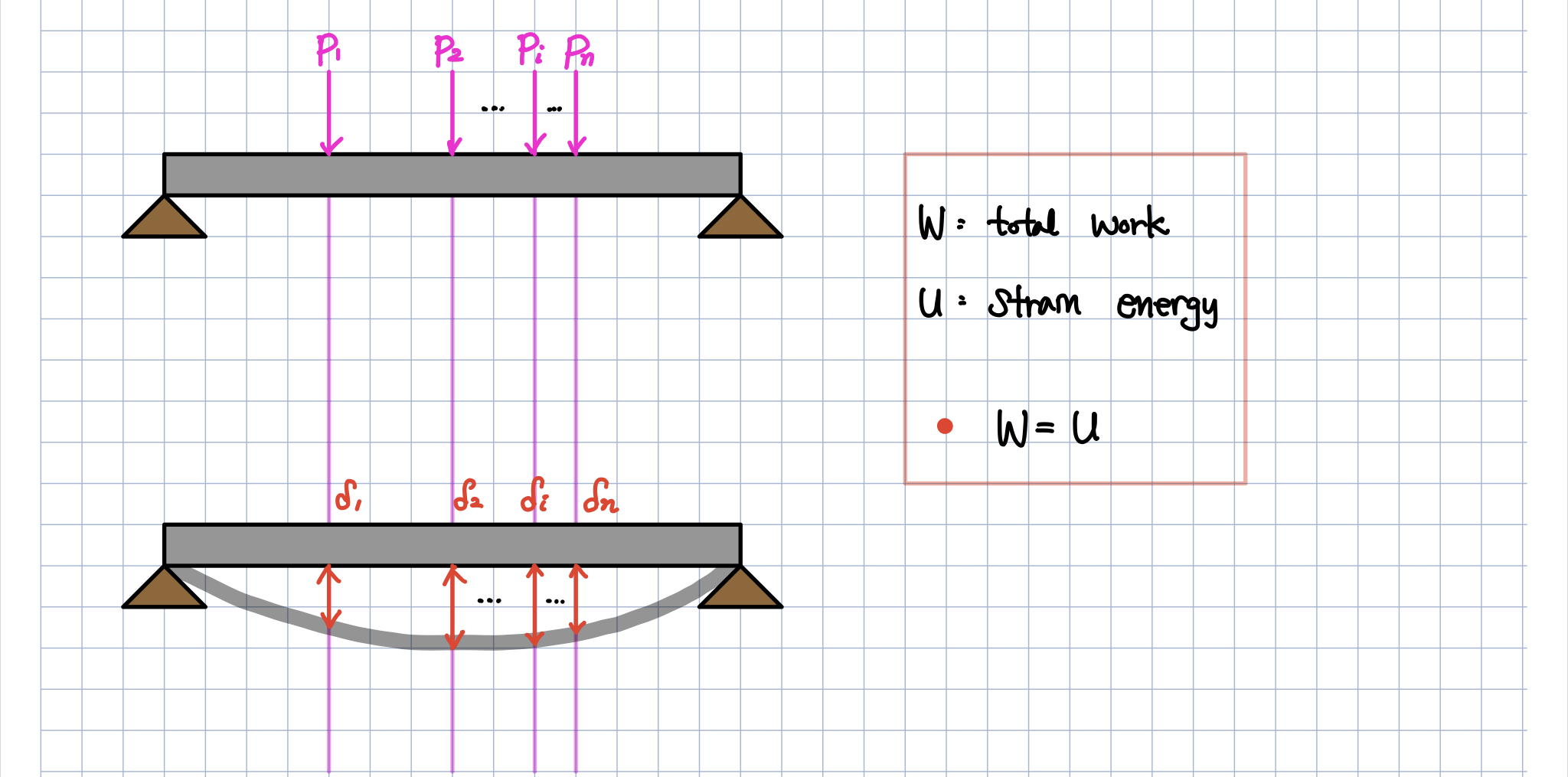
카스틸리아노에서 기억해야할 것은
위에서 보시다시피
dU에 대한 두 가지 표현입니다.
- dU는 U의 하중에 대한 변화량 x 하중의 미소 증가량으로 표현된다. ( dU = \frac{\partial U}{\partial P_i} dP_i )
- dU는 하중이 가해질 때 변형량과의 곱으로 표현될 수 있다. ( dU = \frac{dP_i d\delta_i}{2} + dP_i \delta_i )
위의 내용을 바탕으로
아래와 같이 등식으로 표현하면
우리는 하중에 의한 displacement,
즉 처짐을 계산할 수 있게 됩니다.
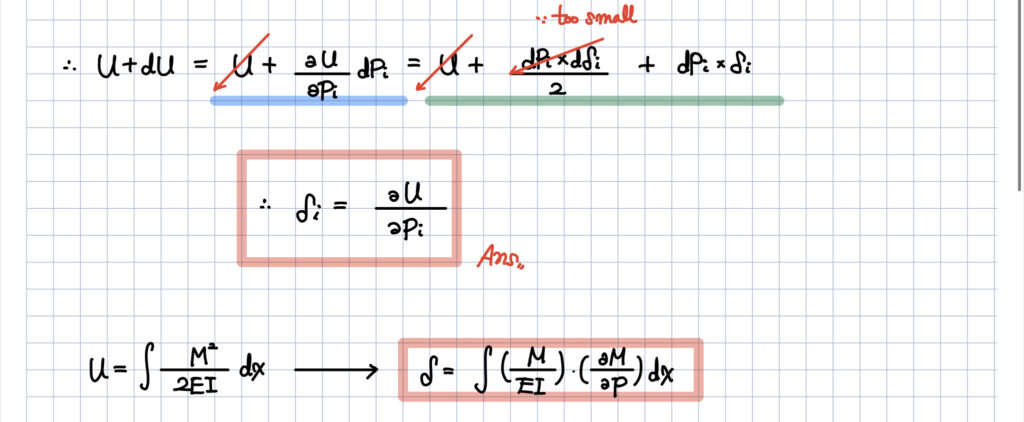
또한 에너지가 모멘트와 강성으로 표현된다는 것을 안다면,
아래와 같이 모멘트와 같이 변형식으로 나타낼 수 있게 됩니다.
직접 문제를 풀어봐야 조금 이해가 쉽겠죠.
수업시간에는 좀더 어려운 문제를 풀어드렸는데
일단 가벼운 문제를 이용해 복습을 해봅시다.
우리는 아래와 같이
cantilever beam 의 끝단의 처짐이 \delta_B =\frac{P L^3}{3 E I} 으로 계산된다는 사실을 이미 알고 있고,
이를 위에서 배운 Castigliano 정리로 구해보도록 하겠습니다.
차근차근 계산하시면,
아래의 모든 과정이 이해되실 겁니다.
만약 이 문제에서 P 가 상수값이라고 할지라도
말씀드린 것처럼
어차피 모멘트 또는 에너지는 P 에 대한 함수일 것이고,
미분이 카스틸리아노 정리로 가능하며,
문제도 쉽게 푸는 것을 확인하실 수 있을 겁니다.

이와 같이 모든 복습과 간단한 예제가
학생 분의 궁금증을 해결했기를 바랍니다.
만약 제가 질문을 잘못 이해했거나
조금 부족한 답변이었다면
다시 질문해주시면 감사하겠습니다.
감사합니다.
카스틸리아노 문제 풀이를 원하시면
링크를 클릭해주세요.