1차원 형태의 filler(i.e. fibers)로 이루어진 복합체(Composite)의 경우, 방향에 따라 modulus 가 달라지게 됩니다. Filler와 Matrix의 volume fraction을 알고, 각 재료의 물성치를 알 때 복합체의 물성치는 어떻게 될 지 같이 알아봅시다.
답변
Kevlar Fiber 에 관한 문제입니다.
먼저 문제를 한번 읽어봅시다.
The Kevlar fibers are aligned all in the same direction in an epoxy matrix. The modulus of the composite is as below;
E = 70 GPa (Parallel)
E = 10 GPa (Perpendicular)
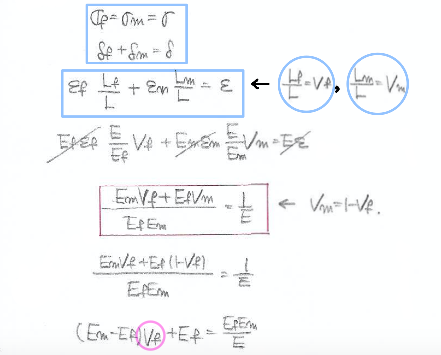
Epoxy: E = 3.5 GPa, \nu = 0.33
Kevlar: E = 124 GPa, \nu = 0.35
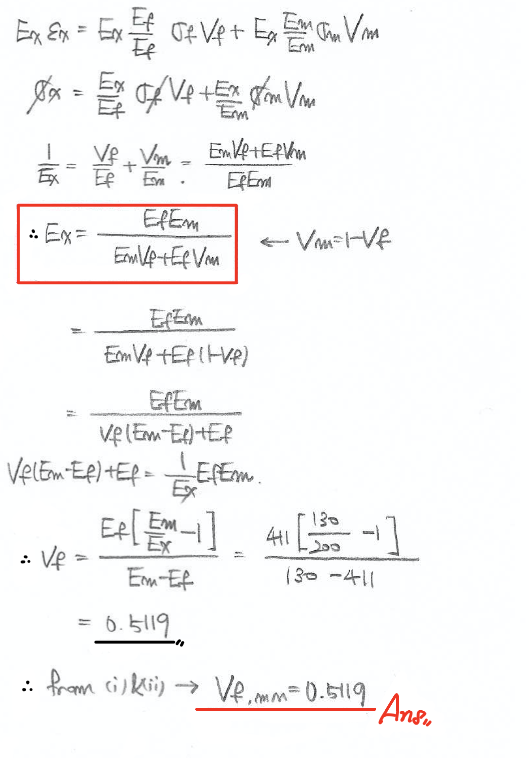
(a) V_f (smallest)
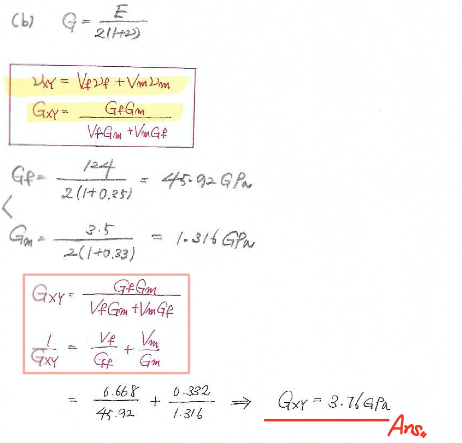
(b) G_{XY} (an estimate of the shear modulus)
(c) \nu_{XY} (the major Poisson’s ratio)
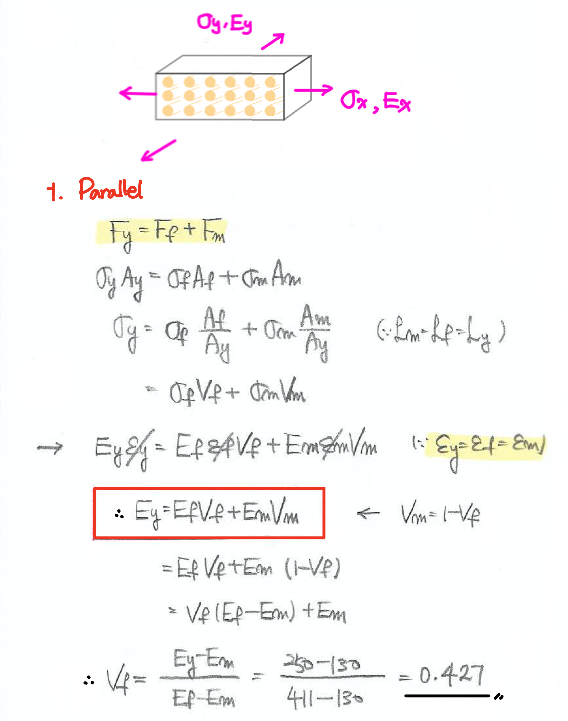
Parallel
힘의 방향과
1차원 filler의 major orientation이 일치할 경우 (평행)
가장 중요하게 기억해야할 것은 아래 파란색으로 네모친 현상입니다.
- 총 힘의 합은 filler와 matrix에 작용하는 힘의 합이다.
- 총 면적의 합은 filler와 matrix에 작용하는 면적의 합이다.
- filler와 matrix의 변형률은 같다.
수직하는 경우와 구분할 수 있다면,
전혀 어려운 내용이 아닐 겁니다.
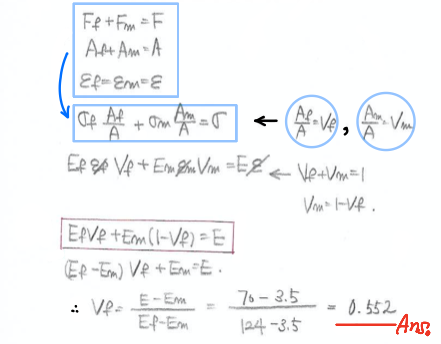
Perpendicular
힘의 방향과
1차원 filler의 major orientation이 수직할 경우
가장 중요하게 기억해야할 것
- 총 응력의 합은 filler와 matrix에 작용하는 응력의 합이다.
- 총 변형량의 합은 filler와 matrix에 작용하는 변형량의 합이다.
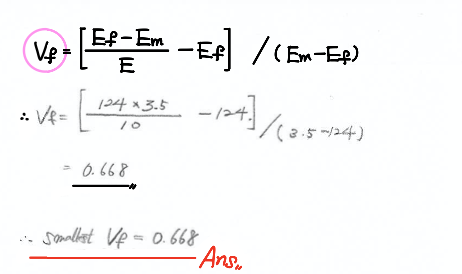
- The Poisson’s ratios
- The shear modulus
위와 비슷한 방법으로
포아송비와 shear modulus를 유추할 수 있습니다.
고체역학 한방에 끝내기 또는 유투브 강의에서
Shear modulus와 elastic modulus 와의 관계를 설명한 바 있습니다.
잊으신 분들은 아래의 영상을 통해 꼭 다시 보시길 바랍니다.
먼저 shear modulus 부터 구해봅니다.
이제 Poisson’s ratio 를 구해봅니다.

다른 문제
갑자기 어려운 개념들이 한꺼번에 많이 나오면서
위의 문제가 조금 어려웠을 것 같기도 합니다.
아래 문제는 조금 더 간단한 내용이니
아래의 문제라도 확실하게 이해할 수 있으면 좋겠습니다.
각 재료의 물성치를 알고
각 방향에 따른 물성치의 최소값을 알고 있는 상태에서의
volume fraction 을 구하는 문제입니다.
문제는 아래와 같습니다.
A composite material = Tungsten wire in a single direction + copper matrix
E > 250 GPa (parallel to fibers)
E > 200 GPa (perpendicular to fibers)
Determine the smallest volume fraction of wires.