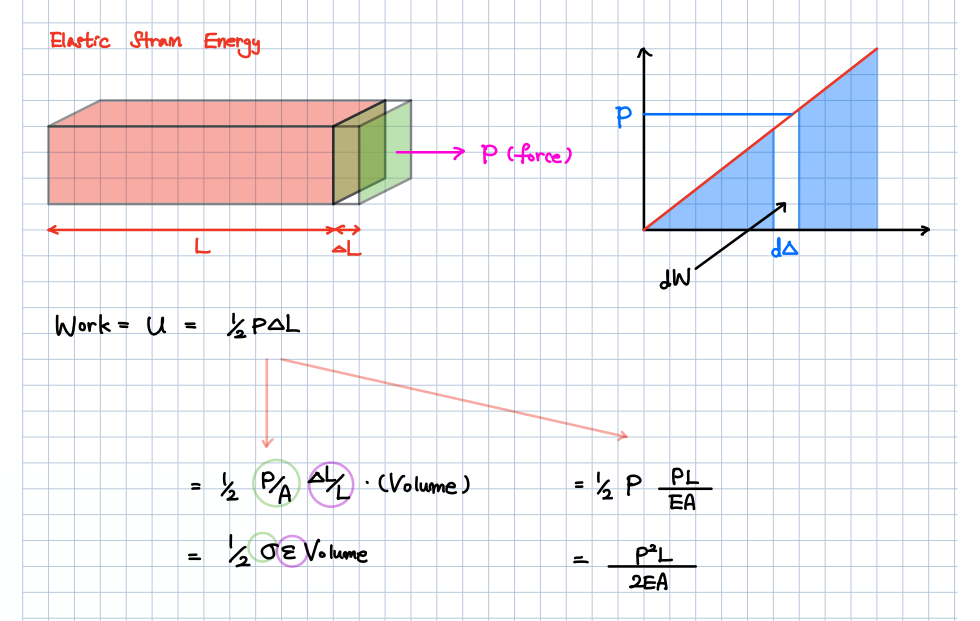
일은 힘x거리인데 1/2를 왜 곱하는건가요? 강의중에 스프링으로 설명을 시작하셨는데 스프링의 일은 1/2kx^2이라하시고 저 봉으로 설명하실 때 W=1/2*p*입실론제곱 이라하셨다가 스프링이 아니라고하시고 제곱만 제거하셨습니다. 1/2도 제거하여야하는거아닌가요? W=1/2*P*입실론=1/2*P*PL/EA=P^2L/2EA 였습니다.
답변
일에 대한 정의를 정확하게 알고,
그 일이 어떻게 유도되는지를 잘 알면 쉽게 해결할 수 있는데요.
학생분께서 생각하시는 것처럼
많은 학생들이 어떤 근거와 논리를 가지고 식을 유도하지 않고,
마치 공식을 외우듯 접근하시는 경우가 많습니다.
예를들어 스프링에너지에서 E = 1/2 k x^2 에서
제곱이 제외됐으니까 1/2도 제거되어야하는 것 아니냐는 질문은
스프링의 일에서 k와 x가 의미하는 것이 정확하게 무엇인지 생각해보지 않았기 때문이라고 생각합니다.
지금부터 다시 Work의 개념을 다시 살펴보고 공부해보도록 합시다.
일 또는 에너지는 말씀하신 것처럼 힘 곱하기 변위가 맞습니다.
다만 시스템에 적요할 때의 핵심은
- 작용하는 힘이 변위에 따라 변하는가?
- 작용하는 힘이 변위에 상관없이 일정한가?
만약 힘이 변위에 따라 일정하게 작용하면 당연히 일은 단순하게 힘 곱하기 거리로 표현할 수 있겠지만,
힘이 변위에 따라 다르다면
적분을 하는 과정 중에 힘이 변위의 함수가 되기 때문에
단순히 곱하면 안되겠습니다.

일에 대한 개념을 알았기 때문에
이를 본격적으로
Elastic Strain Energy에 적용해봅시다.
힘은 길이에 따라 선형적으로 변하기 때문에
힘의 거리에 대한 적분값은
삼각형 형태로 나오기 때문에
1/2이 곱해지구요.
결론적으로 두 가지 strain energy가 유도될 수 있겠습니다.
U = 1/2 P \Delta{L} (적분 후 에너지 값)
U = 1/2 \sigma \epsilon V (stress-strain)
U = \frac{P^2 L}{2EA} (load-displacement)
질문에 대한 답이 됐기를 바랍니다.
다시 한번 말씀드리지만,
절대 단순히 암기식으로 외우지 말고,
왜 식이 이렇게 되는지 물리적으로 이해를 하시길 바랍니다.