Elastic deformation을 배우고 나서 plastic deformation을 배우게 될 때 yield 조건에 대해서 공부를 하게 되는데요. 대표적인 두 조건, Tresca와 von-Mises 조건에 대해서 학생들이 어려워합니다. 사실 매우 간단한 원리인 이 두 조건들이 복잡한 식과 유도과정을 갖고 있기 때문에 결과식만 외우는 학생들이 많은데, 조금만 노력하면 쉽게 모든 과정을 이해할 수 있다고 생각합니다. 천천히, 하나씩 살펴보도록 합시다.
#트레스카 #본미세스 #폰미세스 #고체역학 #항복 #파괴 #응력 #응력해석 #텐서
답변
제가 고체역학 한방에 끝내기에서
가장 자신 있는 두 가지 내용을 고르라고 치면,
- SFD, BMD 그리기
- Mohr’s Circle 그리기
인데요.
제 강의를 들은 친구들 중에 이를 모르는 친구는 정말 없을 겁니다.
안타깝게 고체역학 한방에 끝내기에서 다루지 못했던
Tresca, von-Mises Criterion에 대해서 다뤄볼 예정인데요.
사실 이를 알기 위해서는
- Plane stress
- Stress tensor
- Stress invariants
- Distortion energy theorem
등 많은 내용을 공부하셔야 합니다.
이를 설명하려면 최소한 2시간 정도 추가 강의를 해야 하지만
최대한 이해하기 쉽게 정리해보도록 합시다.
이미 인터넷 상에 많은 내용이 있음에도 불구하고
제가 이렇게 따로 정리하는 이유는
위키피디아나 다른 인터넷 상의 내용들은
학생들이 공부하기엔 식이 너무 많고
이해하기가 어려워서
학습하기에 적합하지는 않다고 생각했기 때문입니다.
제가 아래에 정리한 내용도 식은 매우 많고 복잡하지만
최대한 이해하기 쉽게
다양한 색깔과
깔끔한 정리로 포스팅 했으니
공부에 도움이 되기를 희망해봅니다.
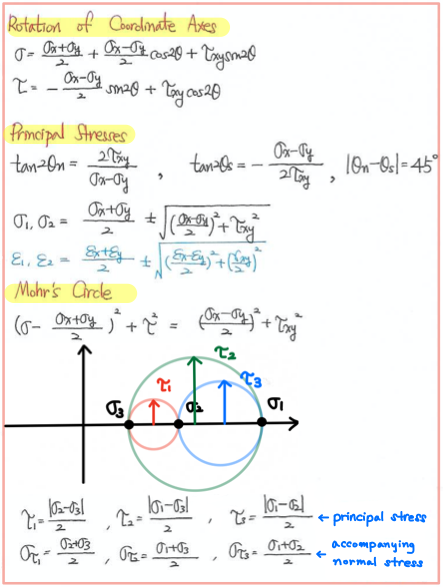
일단 가볍게 Plane stress에 대해서 복습을 해보도록 합시다.

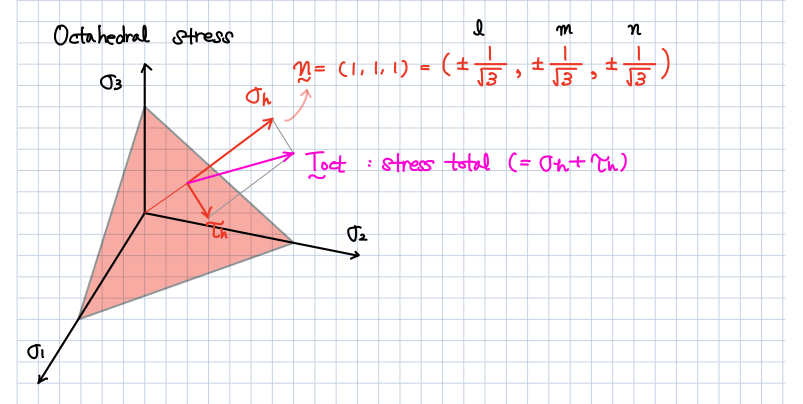
여기서 Octahedral Plane이 나오면서 이게 무슨 소리인가…싶으실 겁니다.
괜찮습니다. 제가 뒤에서 설명하겠습니다.
조금만 더 나아가 Tresca, von-Mises 에 대해서 소개해볼게요.

뭔가 식이 복잡합니다.
결과식만 정리하면 아래의 6가지 식을 이해하시면 됩니다.
- \tau_0 = Max \left\{ \frac{\mid \sigma_1 – \sigma_2 \mid}{2}, \frac{\mid \sigma_2 – \sigma_3 \mid}{2}, \frac{\mid \sigma_3 – \sigma_1 \mid}{2} \right \} (Tresca – shear stress w/ principal stresses)
- \sigma_y = Max \left\{ \mid \sigma_1 – \sigma_2 \mid, \mid \sigma_2 – \sigma_3 \mid, \mid \sigma_3 – \sigma_1 \mid\right \} (Tresca – normal stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
사실 위에 5가지 식만 알면,
문제를 푸는 데에 전혀 문제가 없는데요.
- Principal stress 가 무엇인지
- 식이 어떻게 유도되었는지
- Octahedral plane이 무엇인지
등등을 모른다면
정확히 개념과 이론을 이해한다고 말할 수 없을 것이고,
이를 이용해서 어떤 연구를 진행한다는 것은 불가능할 겁니다.
Tresca vs. von-Mises
1. Tresca (Maximum Shear Stress Yield Crieterion)
Ductile 한 재료의 경우,
yielding 이
재료에 작용하는 maximum shear stress 가 (어느 평면이든 상관 없이)
물체가 가지고 있는 고유 shear stress 물성치 보다 크면
발생한다고 보는 관점이 있는데요.
이를 우리는 Tresca criterion 이라고 부릅니다.
때문에 우리가 위에서 설명한 것처럼 주응력의 차이의 반만큼인
최대의 shear stress 가 yield 발생의 기준이 되는 것이죠.
여기서 조금 더 나아가서
물체의 파괴를 에너지 측면에서 바라봐서
기준을 설정하는 것이 바로 von-Mises criterion이 되겠습니다.
2. Octahedral Shear Stress Yield Criterion (von-Mises criterion)
Ductile 한 재료의
yield 발생의 기준을 세우는
다른 관점으로는 von-Mises 가 있습니다.
이는 바로
octahedral plane에 작용하는 shear stress가
재료의 critical 한 물성치 값을 넘기게 되면
yield가 발생한다고 보는 건데요.
Distortion energy를 이용한다는 측면에서
von-Mises 라고도 하고
distortion energy criterion 이라고 도 합니다.
이를 2차원 평면에서 plot 함으로써
어느 기준이 좀더 conservative (좀더 보수적인 = 좀 더 안전하게 계산된) 한 기준인지
보는 것이 매우 중요합니다.
Tresca 의 경우,
어느 평면이든 상관없이
maximum shear stress 만 계산해주면 되기 때문에
문제 해석이나 풀이가 상당히 간단한 반면에
von-Mises 의 경우,
문제를 푸는 건 식에 값만 대입시켜주면 되니 쉽다고 할 수도 있겠지만,
정확하게 식을 유도하고 이해하는 것은
생각보다 어렵고
많은 학생들이 이해하려고 시도하지도 않는 내용이라고 생각합니다.
고체역학 한방에 끝내기를 수강하시는 여러분들께서는
절대 포기하지 말고
아래의 내용을 천천히 꼼꼼하게 공부하셔서
잘 정리하셨으면 좋겠습니다.
(언젠가는 꼭 강의할 날이 있겠죠! 꼭 강의하고 싶습니다.)
식 유도 과정
가장 먼저 이해하셔야 하는 내용은
Octahedral plane 입니다.

von-Mises criterion은 물체의 yielding은 octahedral shear stress가 항복점에 도달할 때를 기준으로 정합니다.
(Tresca는 maximum shear stress가 항복점에 도달하느냐로 결정하기 때문에 Tresca가 좀더 conservative 한 기준이 됩니다. 식은 비록 간단하지만…)
그림에서 표현한 것처럼
Octahedral plane에서 발생하는 stress total 값은
octahedral normal stress와
octahedral shear stress의 합입니다.
이 관계를 이용해
그리고 principal stresses 을 이용해
Octahedral shear stress를 구할 수 있겠습니다.
위에서 설명한 3번 식이 완성되는 것을 확인할 수 있군요.
- \tau_0 = Max \left\{ \frac{\mid \sigma_1 – \sigma_2 \mid}{2}, \frac{\mid \sigma_2 – \sigma_3 \mid}{2}, \frac{\mid \sigma_3 – \sigma_1 \mid}{2} \right \} (Tresca – shear stress w/ principal stresses)
- \sigma_y = Max \left\{ \mid \sigma_1 – \sigma_2 \mid, \mid \sigma_2 – \sigma_3 \mid, \mid \sigma_3 – \sigma_1 \mid\right \} (Tresca – normal stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
하지만 3번식의 경우는
principal stresses 로만 설명되기 때문에
일반적으로 작용하는 stress 에 관련한 식으로도 이를 표현할 수 있어야 합니다.
아래와 같이
stress tensor와 principal stress를 이용해서
characteristic equation을 만드는 것부터 시작합니다.

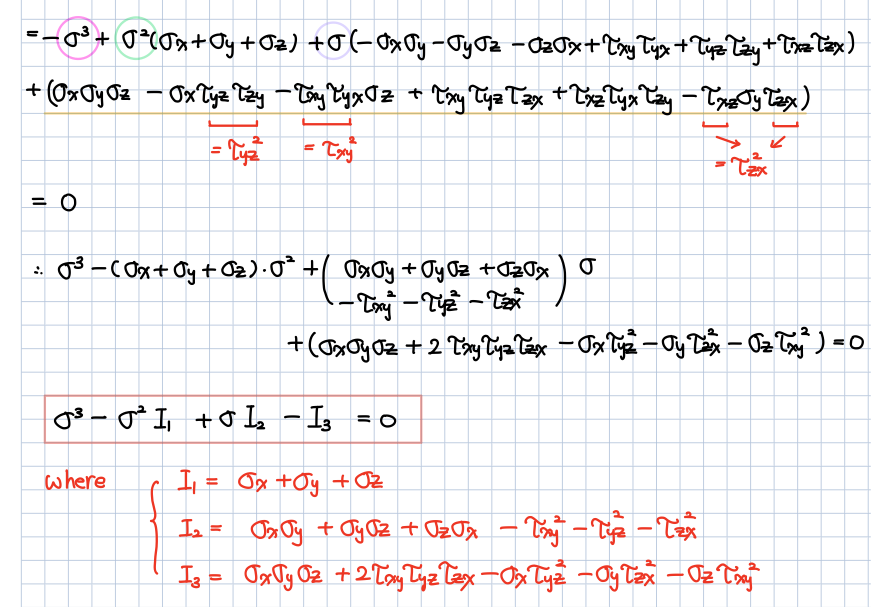
여기서 우리는 stress invariants가 생기는 것을 알 수가 있습니다.
이를 제대로 가르치려면 강의를 해야할 것 같습니다.
쉽게 말해 stress invariants 란
어떤 plane 각도의 변화에도 바뀌지 않는 stress 상태의 고유 조건이라고 할 수 있겠습니다.
첫 번째로 소개한 octahedral stress에 주황색으로 네모친 부분이 있는데 이를 상기하면
아래와 같이 \tau_h 가 stress invariants로 설명이 가능한 것을 알 수가 있습니다.

Stress invariants에 대해서 아직 헷갈리시는 분들이 계실까봐 아래와 같이 다시 정리했습니다.
정말 이렇게 정리하면서도 추가 강의를 하고 싶다는 생각이 듭니다.
이해가 가능하셨으면 좋겠습니다.

결국 위와 같이 octahedral shear stress가
principal stress 뿐만 아니라
일반 stress 로도 표현이 가능한 것을 확인할 수가 있었고,
이는 4번식과 같다는 것을 알 수가 있습니다.
- \tau_0 = Max \left\{ \frac{\mid \sigma_1 – \sigma_2 \mid}{2}, \frac{\mid \sigma_2 – \sigma_3 \mid}{2}, \frac{\mid \sigma_3 – \sigma_1 \mid}{2} \right \} (Tresca – shear stress w/ principal stresses)
- \sigma_y = Max \left\{ \mid \sigma_1 – \sigma_2 \mid, \mid \sigma_2 – \sigma_3 \mid, \mid \sigma_3 – \sigma_1 \mid\right \} (Tresca – normal stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
생각보다 5, 6번 식!
즉 von-Mises에서 normal stress를 유도하는 것을 어려워하는 친구들이 많고
아니, 이 부분에 대해서 유도할 생각을 하는 친구들이 얼마나 있을까 싶기도 합니다.
이를 유도하는 방법에는 여러 가지 방법이 있는데요.
제가 여태까지 공부하면서 가장 쉽다고 느낀 방법은
아래와 같이
- Distortion-Energy Theory
를 이용하는 것이었습니다.
Deformation energy 가 stress 에 의한 energy – hydrostatic pressure 에 의한 energy
임을 아신다면
각각의 stress 에 의한 energy 를 계산할 수 있습니다.
응력과 에너지의 관계에 대해서 아직 헷갈리시는 분들은
아래의 링크를 통해 공부하시길 바랍니다.


Uniaxial yield strength 을 고려해야 하는 조건이라면,
principal stress 에서
1번 축 응력을 제외하고는
나머지 응력은 다 0이 되는 것을 알 수 있기 때문에
제가 위에서 설명한 5번 식이 설명되는 것을 알 수 있었습니다.
3번과 5번의 관계를 통해
4번과 6번의 관계가 성립하므로
위에서 언급한 모든 식이 유도되는 것을 확인할 수 있습니다.
- \tau_0 = Max \left\{ \frac{\mid \sigma_1 – \sigma_2 \mid}{2}, \frac{\mid \sigma_2 – \sigma_3 \mid}{2}, \frac{\mid \sigma_3 – \sigma_1 \mid}{2} \right \} (Tresca – shear stress w/ principal stresses)
- \sigma_y = Max \left\{ \mid \sigma_1 – \sigma_2 \mid, \mid \sigma_2 – \sigma_3 \mid, \mid \sigma_3 – \sigma_1 \mid\right \} (Tresca – normal stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \tau_h = \frac{1}{3} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_1 – \sigma_2)^2 + (\sigma_2 – \sigma_3)^2 + (\sigma_3 – \sigma_1)^2 } (von-Mises – shear stress w/ principal stresses)
- \sigma = \frac{1}{\sqrt{2}} \sqrt{ (\sigma_x – \sigma_y)^2 + (\sigma_y – \sigma_z)^2 + (\sigma_z – \sigma_x)^2 + 6 (\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2)} (von-Mises – shear stress)

내용이 길고 복잡했는데
언젠가 강의할 시간이 생기겠지 생각하면서 정리를 마칩니다.
유도를 바로 공부하기 보다는
문제를 같이 풀면
좀 더 이해가 쉬운데요.
제가 이 내용과 관련한 문제를 많이 준비했으므로
꼭 풀어보시길 바랍니다.
추가 답변 업데이트
아래의 영상들을 통해
추가로 공부해보세요.
영어이긴 하지만,
이해가 충분히 되실 겁니다!