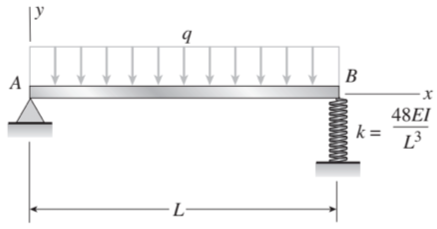
보의 처짐과 처짐각은 이론만 잘 알면 쉬운 내용입니다. 그런데 여기서 딱 한가지가 응용되어 나오는 문제가 있는데요. 바로 보 중간에 힌지 또는 스프링이 달려있는 경우입니다. 스프링이 달려있는 경우도 개념만 알면 너무 쉽게 풀 수 있지만, 많은 학생들이 어려워하여 대표적인 세 문제를 같이 풀어볼까 합니다.
스프링 문제 1
(가장 쉬운 외팔보 유형)
처짐 또는 처짐각의 부호에 대해서
또는 모멘트/전단력의 부호규약에 대해서
다른 포스팅에서 말씀드린 적이 있기 때문에 같이 살펴보시면 좋을 것 같습니다.
아래와 같은 내용으로 적분을 하면 충분히 쉽게 문제를 푸실 수 있으실 겁니다.
처짐과 처짐각을 구하는 그 첫번째 단계는
반발력을 구하고
Bending moment를 구하는 것이겠습니다!
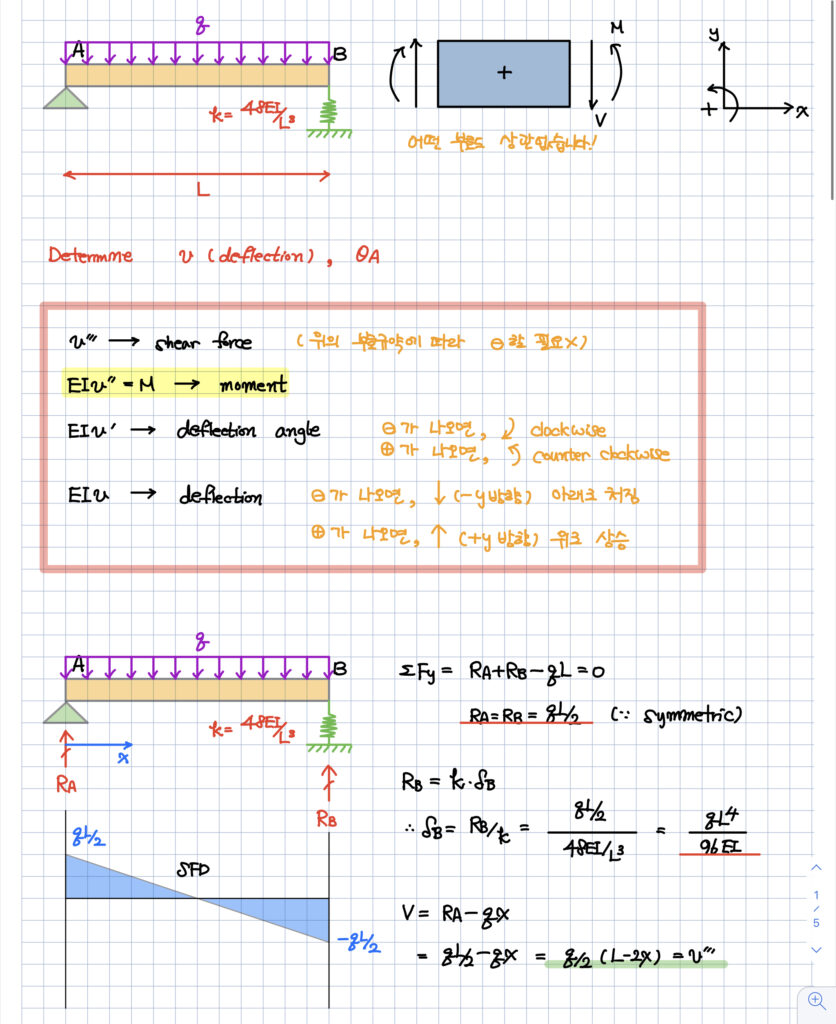
모멘트 또는 전단력 값을 구해서
적분을 하다보면,
처짐과 처짐각도를 쉽게 계산할 수 있습니다.
부호에 최대한 신경을 쓰시고,
적분상수를 구하는 부분에서
실수가 없어야 할 것입니다.

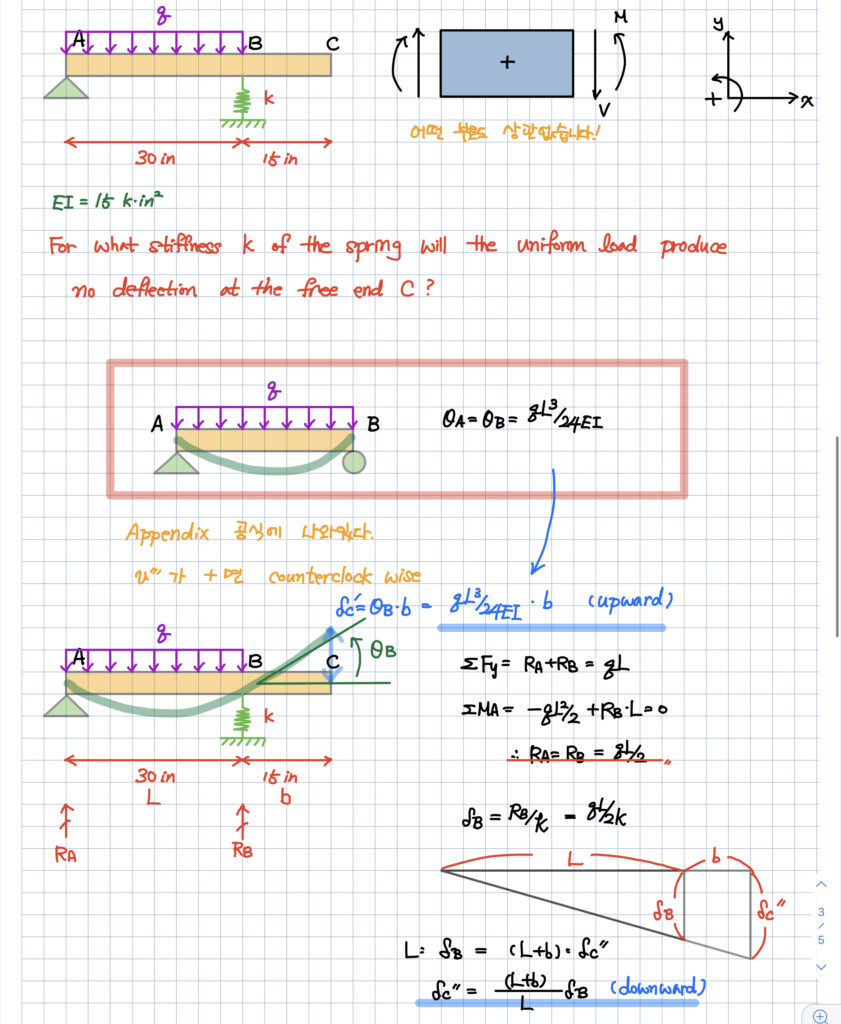
스프링 문제 2
(공식을 활용하는 유형)
만약 처짐각에 대한 공식을 안다면,
아래와 같은 방법으로 구할 수도 있습니다.
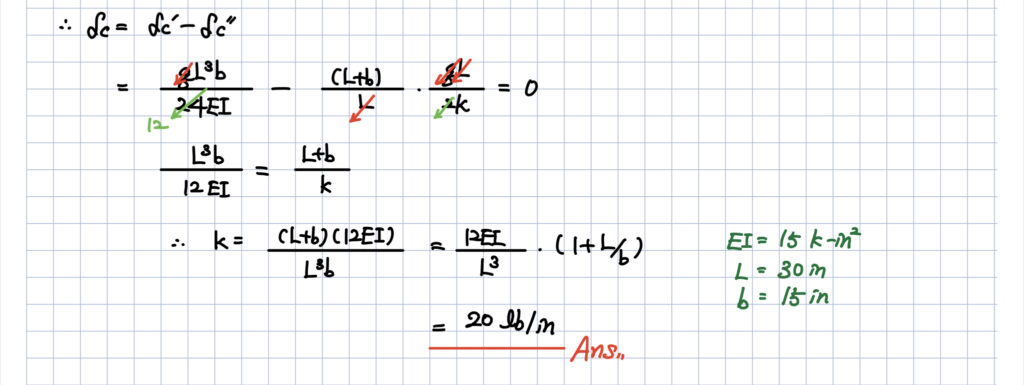
이 문제의 핵심은
C에서의 처짐값을 구할 때 아래의 2가지에 대한 고려가 있어야 한다는 것입니다.
- 스프링에 의한 아래로의 처짐
- 처짐각도에 의한 위로 상승
스프링 문제 3
(카스틸리아노 정리를 활용하는 유형)
공식을 이용하는 방법은 쉬울 수 있으나
제가 역시 별로 좋아하지 않는 방법입니다.
공식을 모르거나 헷갈리면
틀릴 확률이 많기 때문이죠.
차라리 카스틸리아노 정리를 이용하는 방법이
때로는 더욱 쉬울 수 있겠습니다.
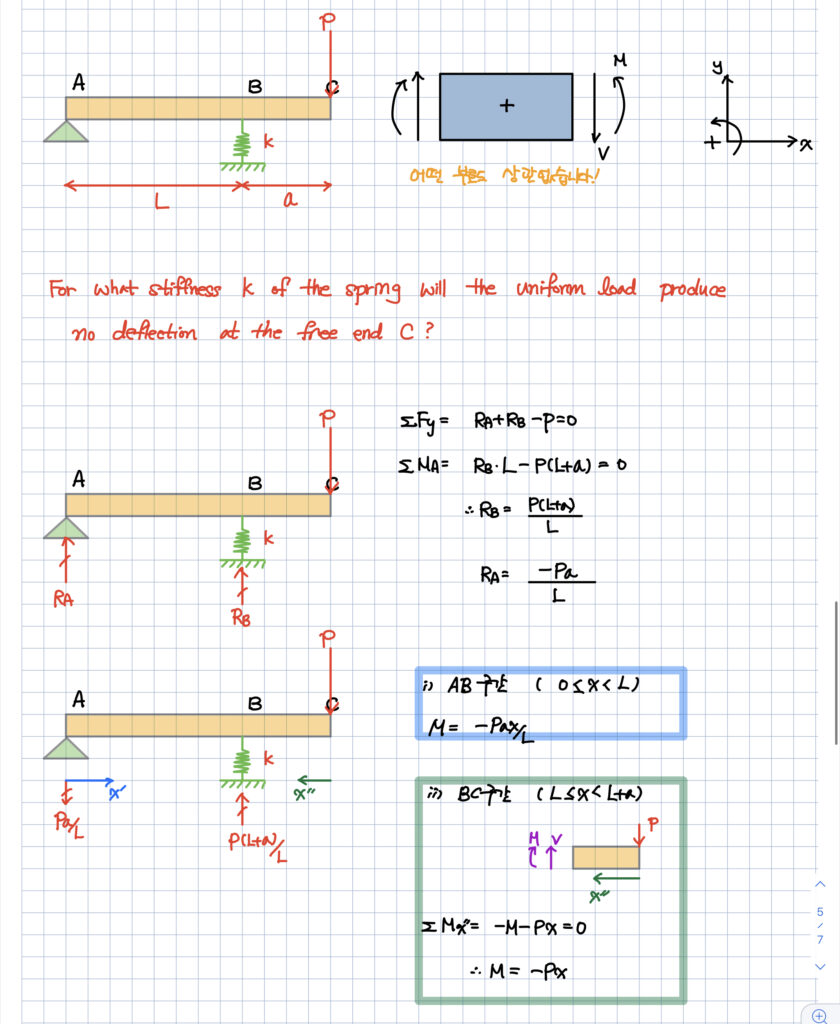
- AB 구간
- BC 구간
으로 구간 별 모멘트를 계산해야 한다는 점을 잘 기억하시고,
strain energy를 계산할 때
- Beam deflection energy
- Spring potential energy
를 고려해줘야 한다는 사실을 잘 이해하시면
쉽게 푸실 수 있습니다.

다양한 방법으로 스프링에 관한 문제를 3개 풀어봤습니다.
이런 식으로 어떤 개념이나 이론이 궁금할 때
시간 투자를 해서
집중적으로 관련 예제를 3-5 문제 정도 풀어보는 것은
내용 이해에 아주 많은 도움이 됩니다.
자주 복습함으로써 내용을 기억하는 것도 중요하니
자주 방문하여 문제를 풀어보시길 바랍니다.