
카테고리: 원하는 부분만 골라! 골라!
순서: 남들이 많이 봤던 내용들만 먼저! 먼저!
키워드 검색: 원하는 내용만 뽑아! 뽑아!
Taylor Series와 Power Series에 대한 이해와 의문점
Taylor Series는 각 항의 계수를 구하는 방법론으로 미분을 제시한 것(양변이 항등식임을 이용하여 수치대입법과 같은 느낌으로 구할 수 있음. 미분을 하지 않은 채로 x_0값을 넣으면 a_0, 미분 한번 한 채로 x_0값을 넣으면 a_1, ... 미분을 n번 한 채로 x_0값을 넣으면 a_n).
고로 Power Series와 Taylor Series는 같은 얘기를 하고 있는 것이라는 결론을 얻을 수 있을 것 같습니다. 임의의 함수가 항상 Power Series로 표현이 가능하다는 엄밀한 증명이 필요하지 않을까 하는 생각도 들었는데, Taylor Series를 통해서 어느 정도 존재성과 유일성이 보여진 것 같네요. x_0가 0인 특수한 경우가 Maclaurin Series가 되겠죠~
그리고 한 가지 의문이 생기는 것이,
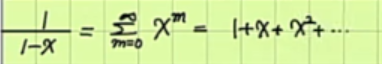
이 문제를 무한등비급수 관점에서 본다면, 공비가 x이고 첫째 항이 1인 무한등비수열의 합이 됩니다. 무한등비수열의 합은 무한등비수열이 수렴할 조건(공비의 절대값이 1보다 작다) 하에서 쓸 수가 있기 때문에, -1<x<1이라는 조건이 필요한데, 막상 좌변을 Maclaurin Series로 표현해보면 우변을 동일하게 얻을 수 있고, 이 때는 x의 범위에 조건이 필요가 없습니다. 두가지의 차이가 어떤 것인지 좀 헷갈리는데, x를 단순히 수로 바라볼 것이냐, 식으로 바라볼 것이냐의 차이인가 싶기도 하고요... 명확한 설명을 해주시면 감사하겠습니다!
Advanced Engineering Mathematics, Erwin Kreyszig
Ch. 1 First-Order ODEs
Ch. 2 Second-Order Linear ODEs
Ch. 3 Higher Order Linear ODEs
Ch. 4 Systems of ODEs. Phase Plane. Qualitative Methods
Ch. 5 Series Solutions of ODEs. Special Functions
Ch. 6 Laplace Transforms
Ch. 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems
Ch. 8 Linear Algebra: Matrix Eigenvalue Problems
Ch. 9 Vector Differential Calculus. Grad, Div, Curl
Ch. 10 Vector Integral Calculus. Integral Theorems
Ch. 11 Fourier series, Integrals, and Transforms
Ch. 12 Partial Differential Equations (PDEs)
Ch. 13 Complex Numbers and Functions
Ch. 14 Complex Integration
Ch. 15 Power Series, Taylor Series
Ch. 17 Conformal Mapping
Ch. 18 Complex Analysis and Potential Theory
아 근데 Taylor Series로 표현이 가능하려면 미분가능한 함수라는 조건이 추가적으로 붙어야겠네요~ 미분이 불가능한 함수도 Power Series로 표현이 가능할지... 그것도 좀 궁금하네요..
일단 저의 답변은 이렇습니다. 정의를 수식으로 써보지 않아서 생긴 질문이다(세상에 어리석은 전공 질문은 없습니다. 이러면서 실력을 기르는 거죠 ㅎㅎ).
1. Power Series와 Taylor Series는 같은 이야기를 하고 있는 것이다?
아닙니다. 다릅니다. 비슷하지만, 엄연히 말하고 있는 바는 다릅니다. 이 부분은 직접 포함 관계(아래 사진의 Example 1을 참고)를 그려보시고, 식을 써보시고 생각하시면 더 좋을 것 같습니다.
2. Maclaurin Series와 무한 등비 급수의 합은 어떻게 다를까요?
먼저, Example 1의 대표적인 Series들의 수식을 한 번 살펴봅시다. Geometric Series는 Maclaurin Series의 Special한 케이스입니다. 그리고 이 Geometric Series 중에 수렴 급수와 발산 급수로 나눠질 수 있겠죠. 그 중에 수렴 급수가 무한 등비급수 입니다. 이때, Geometric Series는 Maclaurin Series보다 하위 포함 관계에 있기 때문에, Geometric Series 만의 조건이 더 붙는 것입니다. 그렇기 때문에 무한 등비급수의 수렴 조건에 따라 이는 Geometric Series에 분류가 되는 것이며, Maclaurin Series는 조금 더 넓은 의미로써, 그 조건이 없어도 충분히 표현이 가능하게 되는 것이죠. 엄밀하게 말해서, 수렴 조건을 따져주는 Geometric Series, 즉 무한 등비 급수를 이용하는 방법이 더 Strict 하다는 것입니다.
3. 미분 불가능한 함수도 Power Series로 표현이 가능할까요?
'미분이 불가능한 함수들 중에, Power Series로 표현이 가능 함수가 존재한다.'라는 명제의 참을 보이고 싶은 상태입니다. 그렇다면, '모든 미분이 불가능한 함수는 Power Series로 표현을 할 수 없다'라는 명제의 반례를 찾으면 증명이 되는 것입니다(한 번 잘 생각해보세요 ㅎㅎ).
그렇다면 이 명제의 대우 명제를 생각해보면, 'Power Series로 표현된 모든 함수는 모두 미분이 가능하다'입니다. Example 2를 보시면, Power Series로 표현된 어떤 함수들은 a_n에 구애받지 않고 모두 모든 점에서 미분이 가능합니다. 따라서 미분 불가능한 함수는 Power Series로 표현이 불가능합니다.
(일단, 이렇게 증명을 하긴 했지만, 명제를 변화 시키는 과정에서 오류가 있었을 수도 있습니다. 제가 다시한 번 쭉 검토하면서, 답변이 바뀐다면 다시 알려드리겠습니다.)
오 일목요연하게 정리를 잘 해주셨네요~ 항상 감사합니다!
Power Series와 Taylor Series가 얘기하는 내용이 다르긴 하지만, 양변이 항등식이라는 점을 이용해 한번씩 미분해가면서 수치대입법을 써가면 결국 Power Series의 표현법은 유일하게 Taylor Series로 나온다고 할 수 있지 않나 싶습니다~
여기서 문제는 Power Series와 Taylor Series를 '항등식으로 둔다'에 있습니다. Power Series는 Taylor Series는 아니지만, Taylor Series는 Power Series입니다. 즉, 포함관계를 잘 생각하셔야 합니다. 항등식으로 둔다라는 것 자체가 Taylor Series의 집합에서 시작한 다는 점입니다. 그러니 당연히 Taylor Series는 무조건 Power Series라는 당연한 결과에 도달하는 겁니다.
제가 반례를 들어보겠습니다. dirac-delta(n-1)을 Power Series의 a_n으로 둬 보겠습니다. Taylor Series의 n!은 상수이니, 뭐 신경쓰지 않아 보겠습니다. 그러면, a_n이 결국에는 0 1 0 0 0 0 ... 을 갖습니다. 앞의 1에서 0을 간 부분은 미분해서 나온 값이라고 주장할 수 있겠지만, 미분해서 0이 1로 나오는 경우는 없죠. 그래서, 반례를 구했습니다. 따라서 Power Series는 Taylor Series가 아닐 수 있습니다.