
카테고리: 원하는 부분만 골라! 골라!
순서: 남들이 많이 봤던 내용들만 먼저! 먼저!
키워드 검색: 원하는 내용만 뽑아! 뽑아!
18강. Two-Degree-of-Freedom Model(Undamped, Modal Analysis)
Ch. 4 Multiple-Degree-of-Freedom Systems
작성자
갓준표
작성일
2024-05-05 14:57
조회
52
#진동학 #권준표
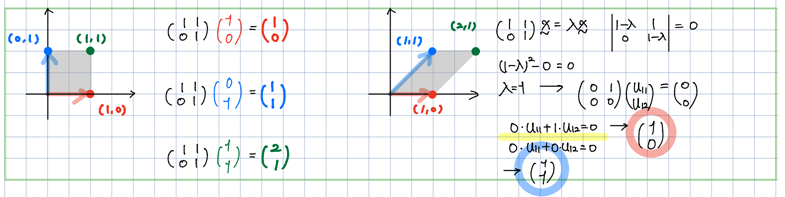
Q1. eigenvector 좌표 (첨부 파일명: eigenvector)
사진처럼 Linear Transformation 후 eigenvalue problem으로 u11, u12를 구한 경우,
제가 1번/2번과 같이 이해했다면 제대로 이해한 것 인가요?
1) u11, u12 = (1 0)
2) u11, u12 = (-1 -1)
1번. 1) 식은 (1,0) (2,0) (3,0) 과 같이 x축으로 커질 수 있다.
- 크기는 바뀌지만 방향 바뀌지 않음 : eigenvector
2번. 2) 식은 (1,1) (2,1) (2,2) (2,3) (3,2) (3,3)과 같이 +x,y축으로 커질 수 있다.
- 크기는 바뀌지만 방향 바뀌지 않음 : eigenvector
따라서, Mode Analysis의 변위(크기)는 정확하지 않고 mode shape(방향)만 알 수 있다.
Q2. eigenvalue problem에서 갑자기 I(Identity matrix, 단위행렬)이 사용되는 이유가 뭔가요?
풀이 후반 대문자 람다(spectral matrix of 틸타K)는 대각행렬로 정의되지만 소문자 람다는 왜 대각행렬로 정의되는 이유가 뭔지 모르겠습니다.

Q3. r에 초기조건 대입 시 r10, r20과 같이 표기 된 것을 n행n열의 의미인 r11, r22로 표기해도 무방한가요? 10, 20으로 명기되어 혼동되는 부분이 있는 것 같습니다.

Q4. mass normalized의 수학적, 물리적 의미가 궁금합니다. 문제 풀이 과정 중 '그렇구나' 하고 넘어갔는데 어떻게 활용되는지 와닿지 않아 질문드립니다.
1) 수학적 의미
2) 물리적 의미
Q1. eigenvector 좌표 (첨부 파일명: eigenvector)
사진처럼 Linear Transformation 후 eigenvalue problem으로 u11, u12를 구한 경우,
제가 1번/2번과 같이 이해했다면 제대로 이해한 것 인가요?
1) u11, u12 = (1 0)
2) u11, u12 = (-1 -1)
1번. 1) 식은 (1,0) (2,0) (3,0) 과 같이 x축으로 커질 수 있다.
- 크기는 바뀌지만 방향 바뀌지 않음 : eigenvector
2번. 2) 식은 (1,1) (2,1) (2,2) (2,3) (3,2) (3,3)과 같이 +x,y축으로 커질 수 있다.
- 크기는 바뀌지만 방향 바뀌지 않음 : eigenvector
따라서, Mode Analysis의 변위(크기)는 정확하지 않고 mode shape(방향)만 알 수 있다.

Q2. eigenvalue problem에서 갑자기 I(Identity matrix, 단위행렬)이 사용되는 이유가 뭔가요?
풀이 후반 대문자 람다(spectral matrix of 틸타K)는 대각행렬로 정의되지만 소문자 람다는 왜 대각행렬로 정의되는 이유가 뭔지 모르겠습니다.

Q3. r에 초기조건 대입 시 r10, r20과 같이 표기 된 것을 n행n열의 의미인 r11, r22로 표기해도 무방한가요? 10, 20으로 명기되어 혼동되는 부분이 있는 것 같습니다.

Q4. mass normalized의 수학적, 물리적 의미가 궁금합니다. 문제 풀이 과정 중 '그렇구나' 하고 넘어갔는데 어떻게 활용되는지 와닿지 않아 질문드립니다.
1) 수학적 의미
2) 물리적 의미
Engineering Vibration, Daniel J. Inman, Pearson
Ch. 1 Introduction To Vibration and the Free Response
Ch. 2 Response To Harmonic Excitation
Ch. 3 General Forced Response
Ch. 4 Multiple-Degree-of-Freedom Systems
Ch. 5 Design for Vibration Suppression
Ch. 6 Distributed-Parameter Systems
Ch. 7 Vibration Testing and Experimental Modal Analysis
Ch. 8 Finite Element Method
[첫 번째 질문에 대한 답변]
eigenvector를 본질적으로 이해하고 싶으신 것 같습니다. 안타깝지만, 무슨 내용을 질문하시는 건지 몰라서 아래와 같이 좀더 이해하기 편하게 제가 대화형으로 내용을 재구성해봤습니다. 진동학에서의 Modal Analysis와 Eigenvector의 의미를 잘 이해할 수 있는 계기가 되기를 바랍니다.
[갓준표 교수] 안녕하세요! 질문해 주셔서 감사해요. 😊 일단, eigenvector와 eigenvalue는 진동 시스템의 기본적인 동작 특성을 이해하기 위해 아주 중요한 요소입니다. 간단히 설명드리면, eigenvalue는 시스템이 자연 진동을 할 때의 진동수를 나타내고, eigenvector는 그 진동수에서 시스템의 모드 형태, 즉 진동하는 모양을 나타냅니다.
진동학에서 modal analysis를 할 때, eigenvalue와 그에 해당하는 eigenvector들은 구조물이 어떻게 진동할지를 알려줍니다. 예를 들어, 다리나 건물 같은 구조물이 지진이나 바람 등 외부 요인에 의해 어떻게 움직일지 예측하는 데에 도움을 줍니다.
eigenvalue가 클수록 해당 mode에서의 진동수가 높으며, 각 eigenvector는 해당 진동수에서의 구조 형태를 보여줍니다. 이런 정보는 구조물의 설계나 안전 검사에서 아주 큰 역할을 합니다. 😄
[학생] 그렇다면 eigenvector가 여러 개 있을 때, 모든 eigenvector들이 구조물의 안전성에 동등하게 중요한가요?
[갓준표 교수] 좋은 질문이네요! 👍 실제로 모든 eigenvector가 같은 중요도를 가지는 것은 아닙니다. 일반적으로 낮은 진동수를 가진 첫 몇 개의 mode가 가장 중요하다고 여겨집니다. 왜냐하면, 실제 운용 중에 구조물이 가장 많이 응답하는 주파수는 일반적으로 낮은 편이기 때문입니다.
또한, 높은 mode의 eigenvector는 보통 더 복잡한 진동 형태를 보이며, 이러한 모드는 일상적인 환경에서는 잘 활성화되지 않습니다. 하지만, 특정 조건 하에서는 높은 mode도 중요할 수 있으니, 전체적인 분석이 중요합니다. 😊
[학생] 그럼 주파수가 낮은 mode만 중요하다면, 그 이상의 모드는 왜 계산하는 건가요?
[갓준표 교수] 아주 핵심적인 질문을 해주셨네요! 🌟 사실 낮은 mode가 일반적으로 가장 중요하지만, 구조물의 전체적인 거동을 이해하기 위해서는 더 높은 mode들도 고려해야 합니다. 이런 높은 mode들은 특수한 상황에서 구조물이 어떻게 반응할 수 있는지, 예를 들어 비정상적인 하중이나 동적 영향을 받을 때, 구조물 거동의 예측에 매우 중요할 수 있습니다. 복합적인 상황에서 구조물의 안전을 확실히 하기 위해, 가능한 모든 시나리오를 분석하는 것이 중요합니다.
[학생] 그러면, 낮은 mode의 eigenvector가 특정 방향의 움직임을 나타낸다고 이해하면 되는 건가요?
[갓준표 교수] 정확하게 이해하셨습니다! 👏 낮은 mode의 eigenvector는 그 방향으로의 움직임이 가장 크게 나타나는 형태를 보여줍니다. 이는 구조물이 해당 방향으로 가장 크게 움직일 때의 상황을 예측할 수 있게 해줍니다. 잘 따라오셨어요. 계속해서 궁금한 점을 질문해주세요!
[두 번째 질문에 대한 답변]
Cholesky Decomposition은 대칭 양의 정부호 행렬 (symmetric positive definite matrix)을 분해하는 기법입니다. 진동학에서는 이 기법을 사용하여 진동 시스템의 고유진동수와 모드 형상을 구할 수 있습니다. 첫 번째 질문과 마찬가지로 이 질문을 주신 이유는 근본적인 Cholesky Decomposition의 사용의의를 묻는 것으로 저는 이해했습니다. 혹시 identity matrix가 사용되는 이유가 단순히 궁금한 것이라면, 진동수의 정보를 가진 람다라는 대각행렬을 수학적으로 처리해주기 위함입니다. 아래의 답변을 좀더 살펴보세요.
특히 진동수가 대각원소로 들어있는 람다행렬의 경우, 대각행렬로 정의되는 이유는 다음과 같습니다:
1. 대칭성: 진동 시스템의 질량, 감쇠, 강성 행렬은 일반적으로 대칭 행렬입니다. 따라서 고유진동수를 구하기 위한 특성방정식에서 얻어지는 고유값 (고유진동수의 제곱)도 대칭 행렬이 됩니다.
2. 정규직교성: 고유모드는 정규직교 벡터 집합을 이루게 됩니다. 이는 고유모드들 간의 직교성을 의미하며, 이로 인해 고유진동수가 대각행렬 형태로 나타나게 됩니다.
3. 진동 모드의 독립성: 대각행렬 형태의 고유진동수는 진동 모드들이 서로 독립적임을 의미합니다. 즉, 한 모드의 진동이 다른 모드에 영향을 미치지 않습니다.
따라서 Cholesky Decomposition을 통해 대칭 양의 정부호 행렬을 분해하면, 고유진동수가 대각원소로 포함된 대각행렬 형태의 람다 행렬을 얻을 수 있습니다. 이는 진동 시스템의 특성을 잘 보여주는 중요한 결과입니다.
[세 번째 질문에 대한 답변]
r10, r20은 각각 1번 또는 1번 물체의 초기값(t=0)의 변위를 의미합니다. 때문에 r11, r22로 기입하는 것은 수학적으로 바람직하지 않습니다.
[네 번째 질문에 대한 답변]
강의에서도 자세하게 설명드렸지만, 뭔가 부족했던 것 같습니다. 아래와 같이 Normalized Mass 행렬의 수학적, 물리적 의미에 대해 자세히 설명드리겠습니다. 마지막 요약 부분은 제가 강의에서도 수차례 강조했던 부분입니다. 꼭 명심하시면서 공부하시면 좋겠습니다.
1. 수학적 의미:
- Cholesky Decomposition은 양의 정부호 행렬(Positive Definite Matrix)을 분해하는 기법입니다.
- 시스템의 질량 행렬 M은 양의 정부호 행렬이므로, Cholesky Decomposition을 통해 M = L * Lᵀ 형태로 분해할 수 있습니다.
- 여기서 L은 하삼각 Cholesky 인자(Cholesky Factor)라고 합니다.
- Normalized Mass 행렬은 이 Cholesky Factor L을 사용해 정의됩니다.
- Normalized Mass 행렬 = L^(-1) * M * L^(-T)
- 이를 통해 정규화된 질량 행렬을 얻을 수 있습니다. 이 행렬은 단위 행렬(Identity Matrix)이 됩니다.
2. 물리적 의미:
- 진동 시스템에서 질량, 감쇠, 강성 행렬은 시스템의 물리적 특성을 나타냅니다.
- 이 중 질량 행렬 M은 가장 기본적인 물리량입니다.
- Normalized Mass 행렬은 질량 행렬 M을 정규화한 행렬입니다.
- 정규화된 질량 행렬은 단위 행렬이 되므로, 시스템의 모드 형상(Mode Shape) 벡터들이 정규직교(Orthonormal)하게 됩니다.
- 이는 모드 해석 시 모드 벡터들이 서로 독립적이며, 질량 행렬 M에 대해 정규화되어 있음을 의미합니다.
- 즉, Normalized Mass 행렬을 사용하면 모드 해석이 수학적으로 단순해지며, 물리적으로도 모드 벡터들이 질량 행렬에 대해 정규화된 상태가 됩니다.
요약하면, Normalized Mass 행렬은 Cholesky Decomposition을 통해 질량 행렬 M을 정규화한 것으로, 수학적으로는 단위 행렬이 되며, 물리적으로는 모드 벡터들이 질량 행렬에 대해 정규화된 상태가 됩니다. 이를 통해 모드 해석 문제가 단순해지는 장점이 있습니다.