β자리에 0이 들어가신다고 하셨는데 이부분 설명을 여러번 들었는데 잘 이해가 안가서요ㅠ 교수님이 설명하신걸 제가 이해한바로는 ‘v’에 해당하는 부분은 ‘CV의 속도’가 들어가는 것이고 ‘β’는 ‘CS로 들어가는 물체의 속도’를 의미해서 a부분에서 Chain은 이미 CV내부에 있으므로 CS에서의 속도가 0이라는 말씀이신가요? 뭔가 이해가 되면서도 안되는것 같아 질문을 드립니다.
동역학에 Kinetics of Systems of Particles 부분에 Reynold’s Transport Theorem 이 나오는데요. 유체역학과 달리 CV 안의 질량이 바뀌는 경우에 대한 문제가 동역학에서 나오기 때문에 많이 헷갈릴 수 있겠습니다. 다시 한번 살펴보도록 하겠습니다.
답변
유체역학의 레이놀즈 수송정리에서 나오는 연속체와는 달리
어떤 유한한 질량을 가지고 있는 시스템이 작동물질로 작용되는 동역학에서의 레이놀즈 수송정리의 경우
많이 헷갈릴 수 있고,
어려운 내용이라고 생각합니다.
제가 이번 기회에 추가로 설명을 드려서
강의에서 부족했던 부분을 보충하고,
학생분의 질문에도 답이 될 수 있도록 하겠습니다.
먼저 레이놀즈 수송정리부터 복습해보겠습니다.
B 라는 것은
우리가 시스템 또는 CV 에 해당하는
임의의 상태량이 될 수 있다고 했는데요.
이 상태량은 CV의 상태에 따라서 다르게 적용돼야 할 것입니다.
CS 적분항에도 \beta 는 들어가는데요,
만약에 모멘텀 방정식이기 때문에
\beta = v 로써 적용이 될 것입니다.
여기서
CS 적분항 안에 있는 \beta = v 와
CV 항에 있는 \beta 를 구분하셔야 합니다.

유체역학 한방에 끝내기에서 제가 설명드린 내용을
비교 차원에서 살펴보도록 하겠습니다.
연속체의 경우
(그리고 별다른 특이 사항이 없는 steady-flow 인 경우)
CV 안의 상태량인 B 또는 \beta 가
시간에 따라 변하지 않고
일정하게 값을 갖고 있는 것을 아실 겁니다.
때문에 시간으로 미분한 \frac{d}{dt} ( \int_{CV} \beta \rho dV) 값이 0가 되어
오로지 CS 안에 해당하는 값만이 고려되어
모멘텀 방정식을 완성하는 것을 확인하실 수 있겠습니다.
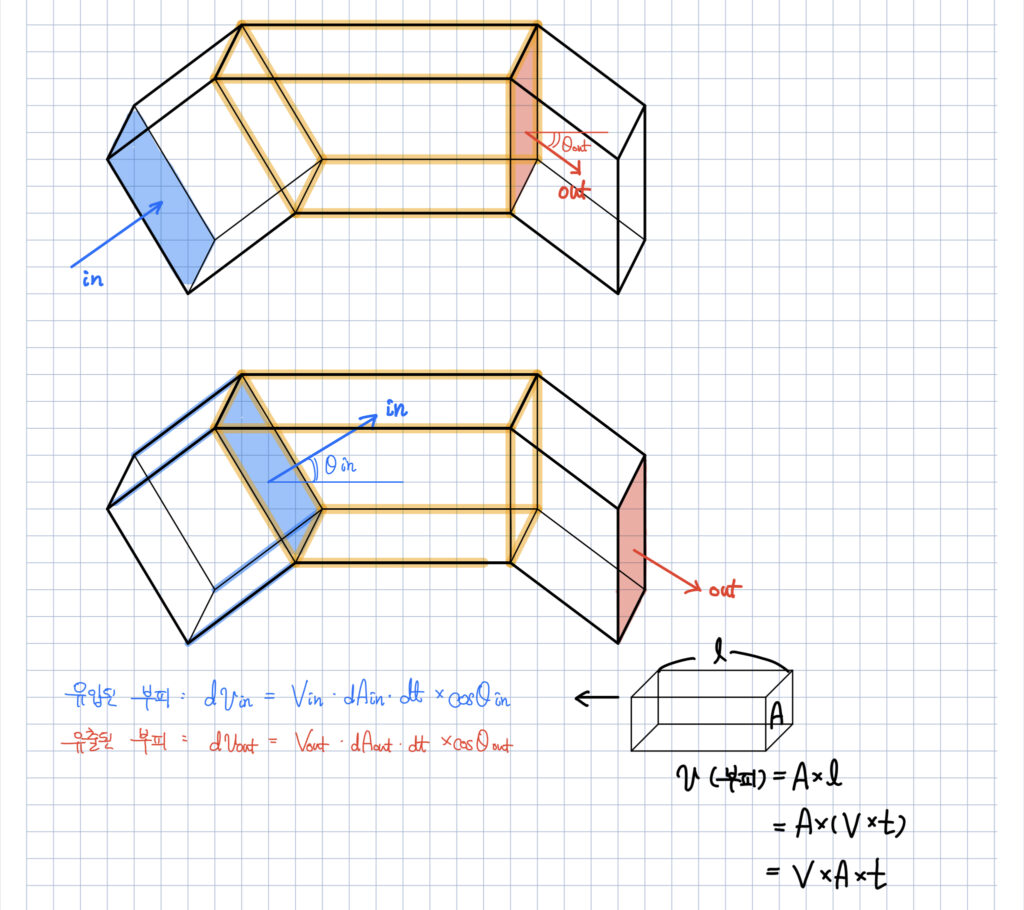
앞서 설명한 모든 내용은
레이놀즈 수송정리의 면벡터를 정리하는 내용에서
자세하게 설명한 바 있기 때문에
혹시라도 관심있으신 분들은
아래의 링크를 통해 강의를 들으시면 좋을 것 같습니다.
서론이 길었습니다.
그렇다면 \frac{d}{dt} ( \int_{CV} \beta \rho dV) 의 값이 0이 되지 않는 경우는
우리가 문제를 어떻게 풀어야 할까요?
즉,
CV 의 질량이 변하거나,
CV 의 속도가 변한다면
어떻게 문제를 풀어야 할까요?
분명 이전과는 다르게 풀어야 할 것 같습니다.
제가 동역학 한방에 끝내기에서
아래와 같이 설명했었는데요.
이 문제는
CV 항의 질량이 바뀌는 경우이기 때문에
CV 항을 0으로 상쇄하지 않고 문제를 풀어야 합니다.
여기서
CV 항을 미분해주는 것과 더불어
또 한가지 중요한 것이 있습니다.
바로 CS 관련 항에 대한 내용입니다.
가장 중요한 핵심은 아래의 내용이었습니다.
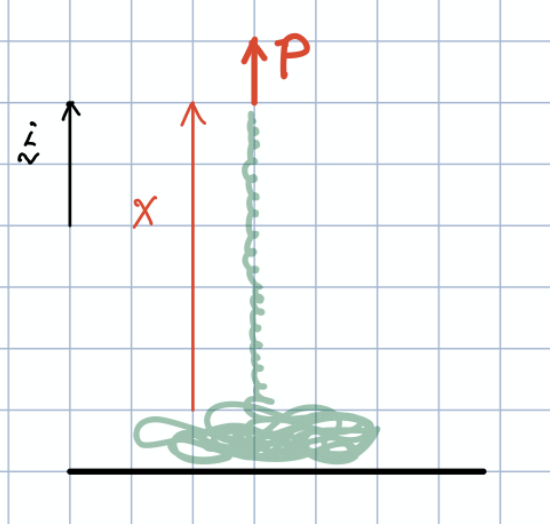
- 초기의 속도가 0이기 때문에 운동량이 0인 chain 들이 들어가서 \beta 값이 0 가 된다.
Chain이 들어가는 속도가 0 이기 때문에
운동량이 0 인 chain 의 질량유량 값은 없다고 볼 수 있을 겁니다.
물론 제가 강의에서 언급하지는 못했는데
CS 가 움직이는 속도도 여기서는 0가 되는데요.
CV 를 아래를 고정한 상태에서
chain 이 위로 계속 들어올려지니까
CV 를 위로 증가하는 식으로 시스템이 설정되기 때문에
CS 의 아랫면의 속도는 0가 되어
속도 값도 0 가 될 것 같습니다. ( \dot{x} = 0 )
어쨌든 CS 관련 항은 0 때문에 없어져서
CV 관련 항만 남아서 문제를 풀 수 있게 됩니다.

다시 말하면,
\beta 의 값은
CS 를 통해 운동량이 0 인 chain 이 들어가기 때문에
0가 되는 것이고,
CS 를 출입하는 속도( v )의 값도 여기서는 0가 되야할 것 같습니다.
CS 에서의 속도가
위/아래에서 모두 0가 되는 이유는
아래의 노란색 상자에
자세하게 표시해뒀으니
꼭 읽어보시길 바랍니다.
아마 이해가 되실 거라 생각합니다.
위의 내용 정리를 바탕으로
아래와 같은 다른 문제도 같이 풀어보면
정리에 도움이 될 것 같습니다.
같은 강의에서 나왔던 문제인데요.
CV 항을 보시면,
CV 사이즈의 증가에 따른 속도가 \beta 값으로 대입된 것을 확인하실 수 있고,
CS 항을 보시면,
(chain 의 경우는 멈춰있다가 들어가는 상황에서 CS 의 출입 속도가 0인 것과 다르게)
이 string 의 문제의 경우,
CS 를 통해 들어가는 질량유량이 \dot{x} 로써 표현되는 것을 확인하실 수 있고,
CS 를 통해 들어가거나 나갈 때 속도를 가지고 있다는 것을
\dot{x} 을 통해
확인하실 수 있을 겁니다.
노란색으로 박스가 쳐있는 부분에서
\beta 가 어떤 값으로 대입되어 있고,
속도가 어떤 값으로 대입되어 있는지 보신다면
chain 문제와의 차이를 분명히 아실 수 있을거라 생각합니다.

같은 강의 마지막에 풀어드린 문제도 마찬가지입니다.
이 문제에서도 마찬가지로
CV 의 \beta 와
CS 의 \beta 를 잘 구분하셔야 합니다.
그리고 이 문제에서는 좀더 주의해서 보셔야 할 것은
CS 를 통해 들어가는 질량유량과
CS 에 유입/유출되는 속도의 차이를 정확하게 아시는 겁니다.
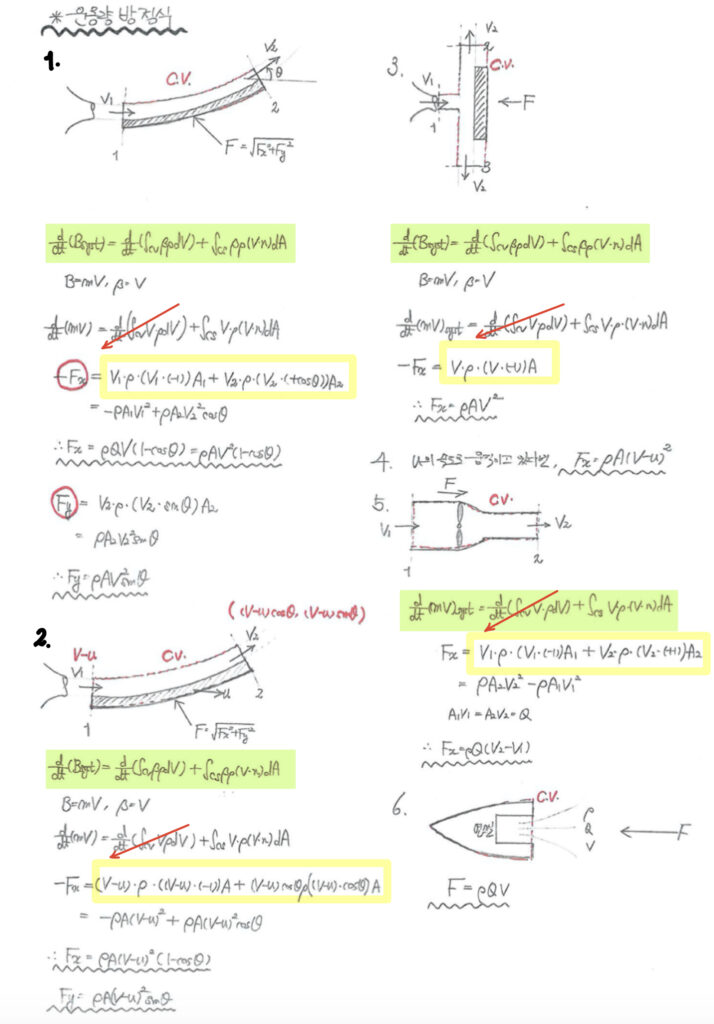
1번 system의 경우
CV: \beta = v_0 (CV 의 속도)
CS: \beta = v (CS 에서 순간적으로 나오는 속도를 통해 계산된 질량유량)
CS: v_1 = v_e = -(v – v_0) (CS 를 통한 유입/유출 속도)
2번 system의 경우
CV: \beta = v (CV 의 속도)
CS: \beta = v (CS 에서 순간적으로 나오는 속도를 통해 계산된 질량유량)
CS: v_2 = v (CS 를 통한 유입/유출 속도)
조금 어렵긴 하지만,
CV 와 CS 의 차이를 이해하고
질량유량과 속도와 연관시켜서 이해하시면
조금 공부하시기 수월하실 것 같습니다.

사실 동역학에서 이런 문제는
그냥 운동량을 넣어서 쉽게 풀 수도 있었을 겁니다.
\Sigma F = m \dot v + \dot m v 를 이용해서 푸는 것이 일반적입니다.
하지만 제 경험을 비추어봤을 때,
정말 어려운 레이놀즈 수송정리의 문제가 나오면
위와 같이 어떤 스칼라 값을 이용해서 구하는 것은 한계가 있다고 생각합니다.
예를 들어 2차원, 3차원 문제를 들 수 있겠습니다.
이렇게 간단한 문제를 왜 이렇게 복잡하게 푸냐는 의견이 있을 수 있지만,
역학과 벡터를 바탕으로
제대로 확실하게 공부하는 것이 장기적으로 볼 때 매우 유익하다고 판단했습니다.
좋은 질문해주셔서 감사합니다.
덕분에 강의를 다시 보면서 제가 실수한 부분을 찾을 수 있었습니다.
항상 좋은 질문 많이 해주시는데 감사합니다.
더욱 좋은 강의로 보답할 수 있도록 노력하겠습니다.
또한 질의응답에 대해
유익하고 효과적인 답변 및 컨텐츠를 통해
학생들의 학습에 도움을 드릴 수 있도록 노력하겠습니다.
감사합니다.